A particle is projected at angle $θ$ with horizontal with velocity $v_{0} a t t = 0$ . Find
(a) tangential and normal acceleration of the particle at $t = 0$ and at highest point of its trajectory.
(b) the radius of curvature $a = 0$ and highest point.
.

Video Solution

Text Solution

Verified by Experts

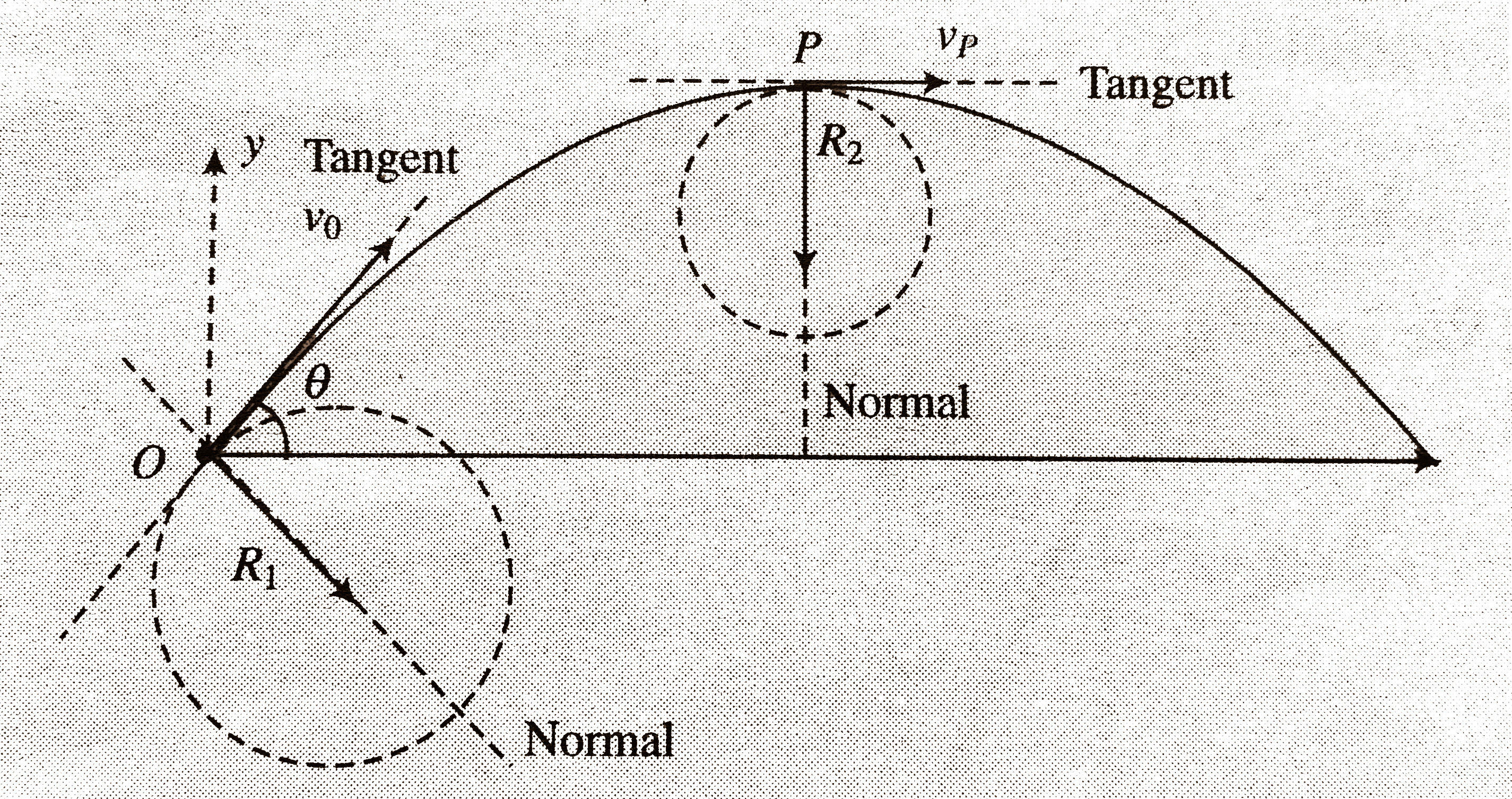
(a) The direction of tangential acceleration is in the line of velocity and the direction perpendicular to velocity direction. The tangential and normal directions at $O and P$ are shown in (Figs. 161 and 5.162), respectively.
The net acceleration of the particle during motion is acceleration due to gravity, i.e., $g$ is acting vertically downward.
At $O (a t t = 0)$ :
Tangential acceleration,
$a_{t} = - g sin θ$
Normal acceleration,
$a_{n} = g cos θ$
At P(at highest point) :
Tangential acceleration,
$a_{t} = 0 and a_{n} = g$
(b) Let the radius of curvature at $O$ be $R_{0}$ . The normal acceleration at $O b e g cos θ$ .
$a_{n} = \frac{v^{2}}{R} \Rightarrow R_{0} = \frac{v_{0}^{2}}{a_{n}} = \frac{v_{0}^{2}}{g cos θ}$
Radius of curvature at $P$ :
Normal acceleration at $P$ is $g$ . Hence,
$R_{P} = \frac{v^{2}}{a_{n}} = \frac{{(v_{0} cos θ)}_{0}^{2}}{g} = \frac{v_{0}^{2} {cos}^{2} θ}{g}$ .
,.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

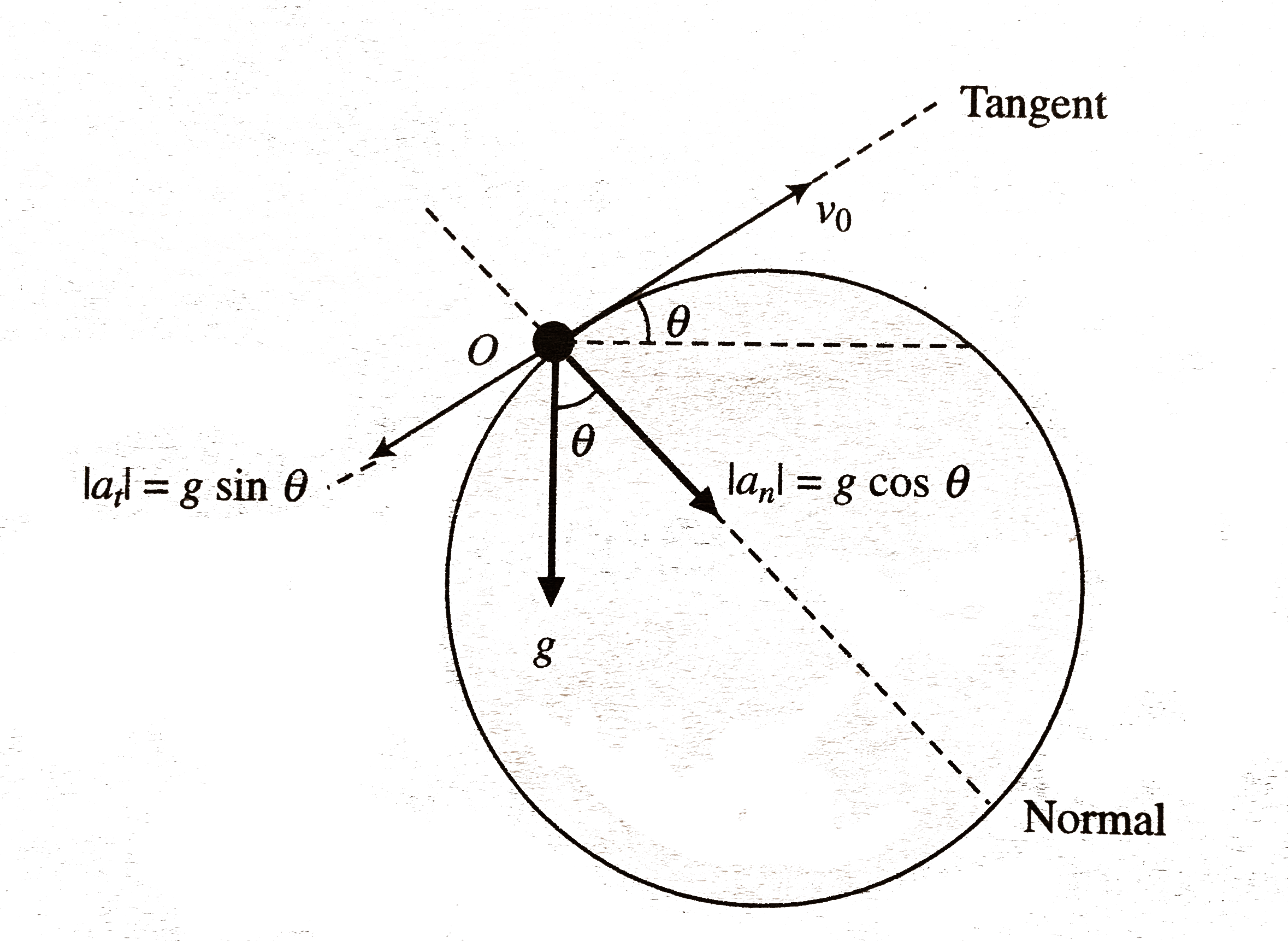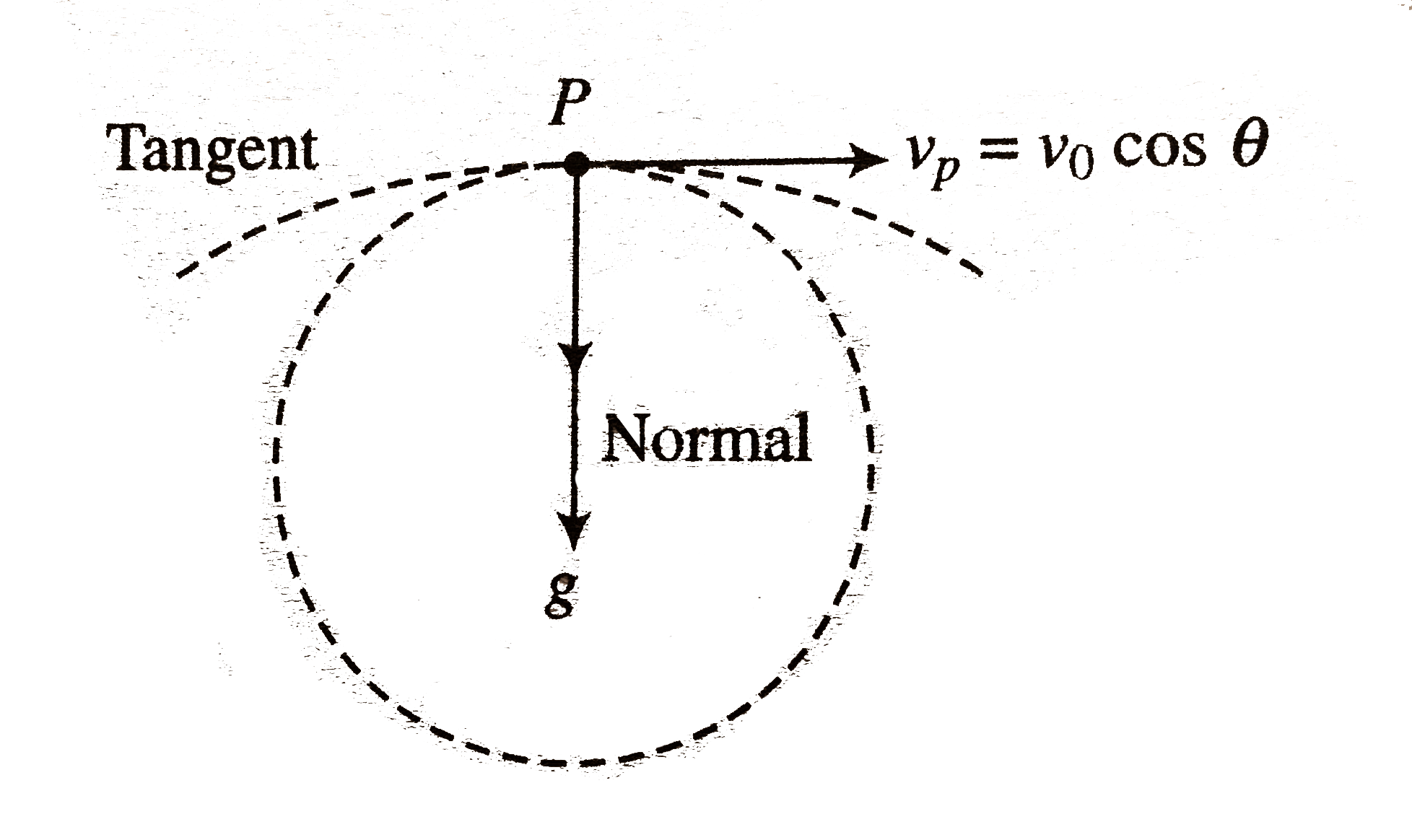Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Exercise Integer

Home
Ask Doubt
Profile