A smooth circular tube of radius is fixed in a vertical plane. A particle is projectid from its lowest point with a velocity just sufficient to carry it to th ehigest point. Show that the time taken by the particle to rach the end of the horizontal diameter is .
Hint :
The correct Answer is:A
To solve the problem, we need to analyze the motion of a particle projected from the lowest point of a smooth circular tube of radius R and determine the time taken to reach the end of the horizontal diameter. Here’s a step-by-step solution:
Step 1: Determine the initial velocity
The particle is projected with just enough velocity to reach the highest point of the circular path. At the highest point, the potential energy is maximum and the kinetic energy is minimum (ideally zero for just reaching the top).
Using the conservation of energy:
12mv20=mg(2R)
where v0 is the initial velocity, m is the mass of the particle, and g is the acceleration due to gravity.
Rearranging gives:
v20=4gR
Thus,
v0=2√gR
Step 2: Relate the angular displacement to time
Let θ be the angle the particle has moved from the vertical. The arc length s traveled by the particle is given by:
s=Rθ
The time dt taken to travel this arc length at velocity v is:
dt=dsv=Rdθv
Step 3: Find the velocity at angle θ
Using conservation of energy again, we can find the velocity v at angle θ:
12mv2=mg(2R−R(1−cosθ))
This simplifies to:
12mv2=mg(R+Rcosθ)
Thus,
v2=2g(R+Rcosθ)=2gR(1+cosθ)
So,
v=√2gR(1+cosθ)
Step 4: Substitute v into the time equation
Substituting v into the equation for dt:
dt=Rdθ√2gR(1+cosθ)
This can be rewritten as:
dt=R1/2√2g⋅dθ√1+cosθ
Step 5: Integrate to find the total time
To find the total time T taken to go from θ=0 to θ=π2:
T=∫π20R1/2√2g⋅dθ√1+cosθ
Using the identity 1+cosθ=2cos2(θ/2):
√1+cosθ=√2cos(θ/2)
Thus,
T=R1/2√2g∫π20dθ√2cos(θ/2)=R1/22√g∫π20sec(θ/2)dθ
Step 6: Evaluate the integral
The integral ∫sec(x)dx=ln|sec(x)+tan(x)|+C. Hence,
∫π20sec(θ/2)dθ=2ln(sec(π4)+tan(π4))=2ln(√2+1)
Step 7: Final expression for time
Substituting back:
T=R1/22√g⋅2ln(√2+1)=R1/2√gln(√2+1)
Thus, the time taken by the particle to reach the end of the horizontal diameter is:
T=√Rgln(1+√2)
The particle is projected with just enough velocity to reach the highest point of the circular path. At the highest point, the potential energy is maximum and the kinetic energy is minimum (ideally zero for just reaching the top).
12mv20=mg(2R)
where v0 is the initial velocity, m is the mass of the particle, and g is the acceleration due to gravity.
v20=4gR
Thus,
v0=2√gR
Let θ be the angle the particle has moved from the vertical. The arc length s traveled by the particle is given by:
s=Rθ
The time dt taken to travel this arc length at velocity v is:
dt=dsv=Rdθv
Using conservation of energy again, we can find the velocity v at angle θ:
12mv2=mg(2R−R(1−cosθ))
This simplifies to:
12mv2=mg(R+Rcosθ)
Thus,
v2=2g(R+Rcosθ)=2gR(1+cosθ)
So,
v=√2gR(1+cosθ)
Substituting v into the equation for dt:
dt=Rdθ√2gR(1+cosθ)
This can be rewritten as:
dt=R1/2√2g⋅dθ√1+cosθ
To find the total time T taken to go from θ=0 to θ=π2:
T=∫π20R1/2√2g⋅dθ√1+cosθ
√1+cosθ=√2cos(θ/2)
Thus,
T=R1/2√2g∫π20dθ√2cos(θ/2)=R1/22√g∫π20sec(θ/2)dθ
The integral ∫sec(x)dx=ln|sec(x)+tan(x)|+C. Hence,
∫π20sec(θ/2)dθ=2ln(sec(π4)+tan(π4))=2ln(√2+1)
Substituting back:
T=R1/22√g⋅2ln(√2+1)=R1/2√gln(√2+1)
T=√Rgln(1+√2)
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Subjective Questions
Explore 2 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:JEE Main
Explore 23 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Comprehension Based
Explore 5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA particle is projected from point P with velocity 5√2ms−1 prependicular to the surface of a hollow right angle cone whose axis is vertical . It collides at Q normally. The time of the flight of the particle is .

View SolutionA particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

If m2 again comes down and collides with m1 then after the collision
View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

Find the ratio m1:m2
View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?
What is the coefficient of restituting between the beads?
View SolutionAssume that a frictionless tunnel is made in the earth along its diameter, a particle in projected in the tunnel from the surface of the earth with an initial speed v0=√gR, where g is the acceleration due to gravity on the earth's surface & R is the radius of the earth, if time taken by the particle to reach the centre of the earth is πn√4Rg the value of n is?
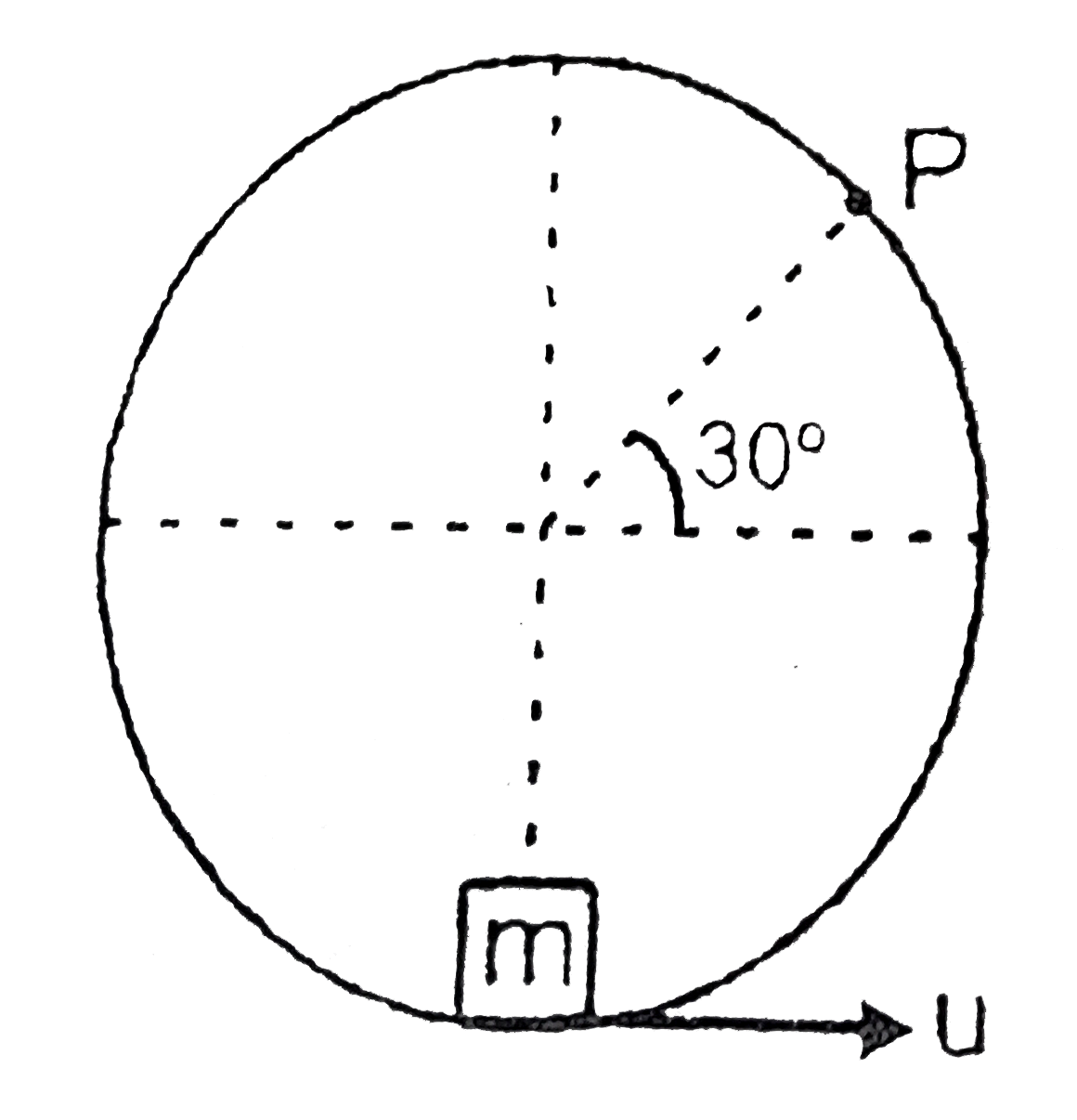
View SolutionA horizontal cylinder is fixed, its inner surface is smooth and its radius is R. A small block is initially at the lowest point. The minimum velocity that should by given to the block at the lowest point, so that it can just cross the point P is u then
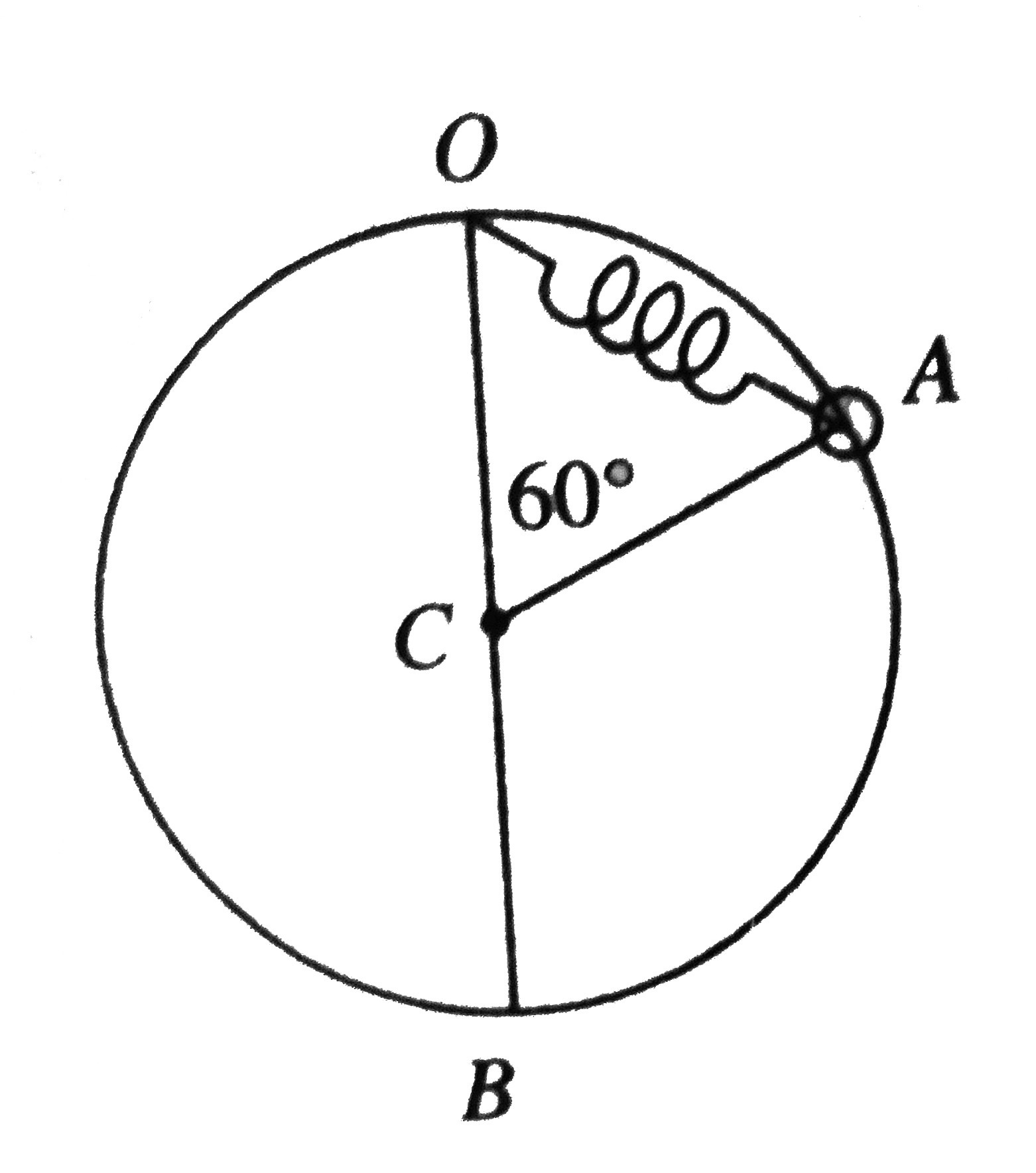
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
View Solution