A table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from the centre becomes L.
ω√L2−a2
ω√a2−L2
ω√2L2−a2
ω√L2
The correct Answer is:A, B
To solve the problem step by step, we will analyze the motion of the particle placed in the groove of the rotating table.
Step 1: Understand the system
We have a table rotating with an angular speed ω. A particle is placed in a groove at a distance a from the center of the table. As the table rotates, the particle will move outward along the groove until it reaches a distance L from the center.
Hint: Visualize the setup. The particle experiences circular motion due to the rotation of the table.
Step 2: Write the expression for centripetal acceleration
The centripetal acceleration ac experienced by the particle at a distance x from the center is given by:
ac=ω2x
Hint: Remember that centripetal acceleration depends on the distance from the center and the angular speed.
Step 3: Relate acceleration to velocity
We know that centripetal acceleration can also be expressed as:
ac=dvdt
where v is the tangential speed of the particle. Thus, we can write:
dvdt=ω2x
Hint: You can think of dvdt as how the speed changes with time as the particle moves outward.
Step 4: Use the chain rule
To relate the change in velocity to the change in position, we can use the chain rule:
dvdt=dvdx⋅dxdt
Since dxdt=v (the speed of the particle), we can rewrite the equation as:
dvdt=vdvdx
Hint: This step involves using the relationship between velocity and position to express the acceleration in terms of position.
Step 5: Set up the equation
Now we can equate the expressions for centripetal acceleration:
vdvdx=ω2x
Rearranging gives:
vdv=ω2xdx
Hint: This equation relates the change in speed to the change in position along the groove.
Step 6: Integrate both sides
We need to integrate both sides to find the relationship between speed and position. The limits for v will be from 0 to v (initial speed to final speed), and for x from a to L:
∫v0vdv=∫Laω2xdx
This results in:
v22=ω2(L22−a22)
Hint: When integrating, remember to apply the limits correctly.
Step 7: Solve for v
Now we can simplify and solve for v:
v22=ω22(L2−a2)
Multiplying both sides by 2 gives:
v2=ω2(L2−a2)
Taking the square root:
v=ω√L2−a2
Hint: The final expression gives the speed of the particle when it reaches distance L from the center.
Final Answer
The speed of the particle as its distance from the center becomes L is:
v=ω√L2−a2
We have a table rotating with an angular speed ω. A particle is placed in a groove at a distance a from the center of the table. As the table rotates, the particle will move outward along the groove until it reaches a distance L from the center.
The centripetal acceleration ac experienced by the particle at a distance x from the center is given by:
ac=ω2x
We know that centripetal acceleration can also be expressed as:
ac=dvdt
where v is the tangential speed of the particle. Thus, we can write:
dvdt=ω2x
To relate the change in velocity to the change in position, we can use the chain rule:
dvdt=dvdx⋅dxdt
Since dxdt=v (the speed of the particle), we can rewrite the equation as:
dvdt=vdvdx
Now we can equate the expressions for centripetal acceleration:
vdvdx=ω2x
Rearranging gives:
vdv=ω2xdx
We need to integrate both sides to find the relationship between speed and position. The limits for v will be from 0 to v (initial speed to final speed), and for x from a to L:
∫v0vdv=∫Laω2xdx
This results in:
v22=ω2(L22−a22)
Now we can simplify and solve for v:
v22=ω22(L2−a2)
Multiplying both sides by 2 gives:
v2=ω2(L2−a2)
Taking the square root:
v=ω√L2−a2
The speed of the particle as its distance from the center becomes L is:
v=ω√L2−a2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
View Solution_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle for that place.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
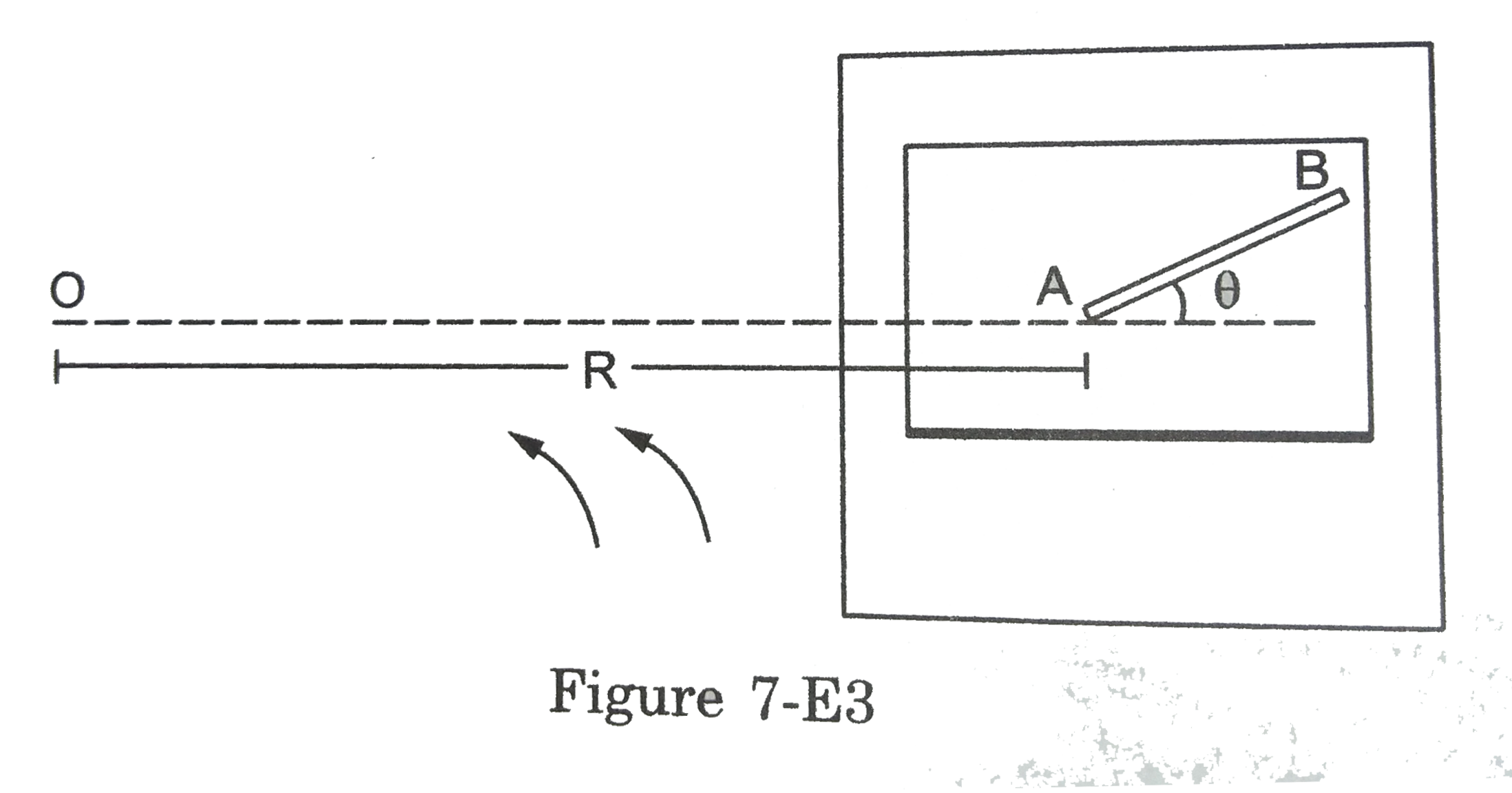
View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.

View SolutionA wheel is rotating at an angular speed ω about its axis which is kept vertical. An identical wheel initially at rest is gently dropped into the same axle and the two wheels start rotating with a common angular speed. Find this common angular speed.
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionA rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.

View Solution
