A river of width 100 m is flowing with a velocity of 1.5 m/s. A man start from one end with rest relative the river. He raws with an acceleration of 2m/s2 relative to the river. If the man want to cross the river in minimum time, by how much distance (in meters) will he be drifted (flown) in the direction of river flow during the crossing.
The correct Answer is:15
To solve the problem of how much distance the man will be drifted downstream while crossing the river, we can break it down into a series of steps:
Step 1: Understand the Problem
The man is trying to cross a river that is 100 meters wide. The river flows with a velocity of 1.5 m/s. The man starts from rest relative to the river and accelerates at 2 m/s² perpendicular to the river. We need to find out how far downstream he will be drifted while crossing the river in minimum time.
Step 2: Determine the Time to Cross the River
To find the time taken to cross the river, we use the second equation of motion:
s=ut+12at2
Where:
- s is the displacement (100 m, the width of the river),
- u is the initial velocity (0 m/s, since he starts from rest),
- a is the acceleration (2 m/s²),
- t is the time taken.
Plugging in the values:
100=0⋅t+12⋅2⋅t2
This simplifies to:
100=t2
Thus:
t=√100=10 seconds
Step 3: Calculate the Drift
The drift in the direction of the river flow can be calculated using the velocity of the river and the time taken to cross:
Drift=Velocity of the river×Time
Where:
- Velocity of the river = 1.5 m/s,
- Time = 10 seconds.
Calculating the drift:
Drift=1.5m/s×10s=15meters
Final Answer
The man will be drifted 15 meters downstream while crossing the river.
---
The man is trying to cross a river that is 100 meters wide. The river flows with a velocity of 1.5 m/s. The man starts from rest relative to the river and accelerates at 2 m/s² perpendicular to the river. We need to find out how far downstream he will be drifted while crossing the river in minimum time.
To find the time taken to cross the river, we use the second equation of motion:
s=ut+12at2
Where:
- s is the displacement (100 m, the width of the river),
- u is the initial velocity (0 m/s, since he starts from rest),
- a is the acceleration (2 m/s²),
- t is the time taken.
100=0⋅t+12⋅2⋅t2
This simplifies to:
100=t2
Thus:
t=√100=10 seconds
The drift in the direction of the river flow can be calculated using the velocity of the river and the time taken to cross:
Drift=Velocity of the river×Time
Where:
- Velocity of the river = 1.5 m/s,
- Time = 10 seconds.
Drift=1.5m/s×10s=15meters
The man will be drifted 15 meters downstream while crossing the river.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.68
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.69
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.66
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View SolutionA river of width 80m is flowing at 6 m/s. A motorboat crosses the river in 10s and reaches a point directly across on the other river bank. The velocity of motorboat in still water is :
View Solution
A river of width d is flowing with a velocity u. A person starts from point A. He always try to keep himself along y axis. Speed of man w.r.t to river at any position is given by v=k√y(k→+ve constant). Time taken by man to cross the river is (Assume that at t=0,y=0)
View SolutionA river is flowing with a velocity of 2m/s. If the width of river in 100 m and swimmer wants to cross river is shortest time, what time (in sec) would he take if velocity of swimmer in still water is 4 m/s ?
View SolutionVelocity of boat in still water is 13 m/s. If water flows ina river with a velocity of 5 m/s. What is the difference in times taken by him to cross the river in the shortest path and in the shortest time. If the width of the river is 10 m.
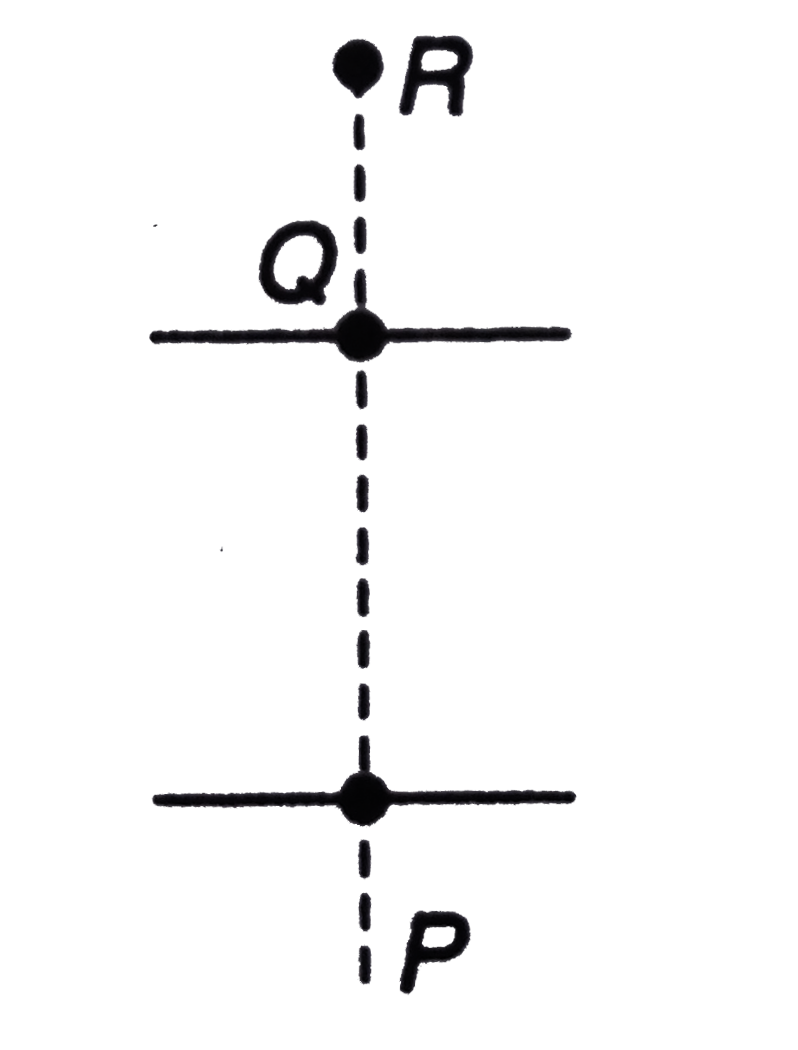
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View SolutionA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
View SolutionThe velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View Solution
