A railway carriage of mass Mc filled with sand of mass Ms moves along the rails. The carriage is given an impulse and it starts with a velocity v0. At the same time it is observed that the sand starts leaking through a hole at the bottom of the carriage at a constant mass rate λ. Find the distance at which the carriage becomes empty and the velocity attained by the carriage at that time. (Neglect the friction along the rails).
To solve the problem, we need to analyze the motion of the railway carriage filled with sand as it loses mass due to the sand leaking out. We will use the principles of conservation of momentum and kinematics.
1. Initial Conditions:
- The initial mass of the carriage is Mc+Ms, where Mc is the mass of the carriage and Ms is the mass of the sand.
- The initial velocity of the carriage is v0.
- The sand leaks out at a constant mass rate λ.
2. Mass of the Carriage Over Time:
- As the sand leaks out, the mass of the carriage at time t can be expressed as:
M(t)=Mc+Ms−λt
- The carriage will become empty when M(t)=Mc, which occurs when:
Ms−λt=0⇒t=Msλ
3. Velocity of the Carriage Over Time:
- According to the conservation of momentum, the momentum of the system must remain constant if no external forces act on it. The initial momentum is:
Pinitial=(Mc+Ms)v0
- The momentum at time t when the mass is M(t) and the velocity is v(t) is:
Pfinal=M(t)v(t)=(Mc+Ms−λt)v(t)
- Setting the initial momentum equal to the final momentum gives:
(Mc+Ms)v0=(Mc+Ms−λt)v(t)
- Rearranging for v(t):
v(t)=(Mc+Ms)v0Mc+Ms−λt
4. Finding the Distance Traveled:
- The distance traveled by the carriage while the sand is leaking out can be calculated by integrating the velocity over the time interval from 0 to t=Msλ:
S=∫Msλ0v(t)dt
- Substituting v(t):
S=∫Msλ0(Mc+Ms)v0Mc+Ms−λtdt
- This integral can be solved using the substitution method or recognizing it as a standard integral form:
S=(Mc+Ms)v0(−1λln(Mc+Ms−λt))Msλ0
- Evaluating the limits gives:
S=(Mc+Ms)v0(−1λ(ln(Mc)−ln(Mc+Ms)))
- Simplifying this yields:
S=(Mc+Ms)v0λln(Mc+MsMc)
5. Final Results:
- The distance at which the carriage becomes empty is:
S=(Mc+Ms)v0λln(Mc+MsMc)
- The final velocity when the carriage is empty (at t=Msλ):
v(Msλ)=(Mc+Ms)v0Mc
- The initial mass of the carriage is Mc+Ms, where Mc is the mass of the carriage and Ms is the mass of the sand.
- The initial velocity of the carriage is v0.
- The sand leaks out at a constant mass rate λ.
- As the sand leaks out, the mass of the carriage at time t can be expressed as:
M(t)=Mc+Ms−λt
- The carriage will become empty when M(t)=Mc, which occurs when:
Ms−λt=0⇒t=Msλ
- According to the conservation of momentum, the momentum of the system must remain constant if no external forces act on it. The initial momentum is:
Pinitial=(Mc+Ms)v0
- The momentum at time t when the mass is M(t) and the velocity is v(t) is:
Pfinal=M(t)v(t)=(Mc+Ms−λt)v(t)
- Setting the initial momentum equal to the final momentum gives:
(Mc+Ms)v0=(Mc+Ms−λt)v(t)
- Rearranging for v(t):
v(t)=(Mc+Ms)v0Mc+Ms−λt
- The distance traveled by the carriage while the sand is leaking out can be calculated by integrating the velocity over the time interval from 0 to t=Msλ:
S=∫Msλ0v(t)dt
- Substituting v(t):
S=∫Msλ0(Mc+Ms)v0Mc+Ms−λtdt
- This integral can be solved using the substitution method or recognizing it as a standard integral form:
S=(Mc+Ms)v0(−1λln(Mc+Ms−λt))Msλ0
- Evaluating the limits gives:
S=(Mc+Ms)v0(−1λ(ln(Mc)−ln(Mc+Ms)))
- Simplifying this yields:
S=(Mc+Ms)v0λln(Mc+MsMc)
- The distance at which the carriage becomes empty is:
S=(Mc+Ms)v0λln(Mc+MsMc)
- The final velocity when the carriage is empty (at t=Msλ):
v(Msλ)=(Mc+Ms)v0Mc
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Now answer the following :20videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 89 illustration5videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 876videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
View SolutionA constant force(F) is applied on a stationary particle of mass 'm'. the velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA cart loaded with sand moves along a horizontal floor due to a constant force F coinciding in direction with cart's velocity vector. In the process, the sand spills through a hole in the bottom with a constant rate μkg/s. Find the acceleration and velocity of the cart at the moment t, if at the initial moment t=0 the cart with loaded sand had mass m0 and its velocity was equal to zero. Friction is to be neglected.
View SolutionA body of mass m slides down an incline and reaches the bottom with a velocity v. If the same mass were in the form of a ring which rolls down this incline, the velocity of the ring at the bottom would have been
View SolutionA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View SolutionTwo girls of equal mass m jump off from the border line of a stationary carriage of mass M with same horizontal velocity u relative to the carriage in same direction. Neglect the effect of friction. Mark correct options.
View SolutionA rail road car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man aproaching the engine?
View SolutionA body of mass m moving with velocity 3km/h collides with a body of mass 2m at rest. Now, the combined mass starts to move with a velocity
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
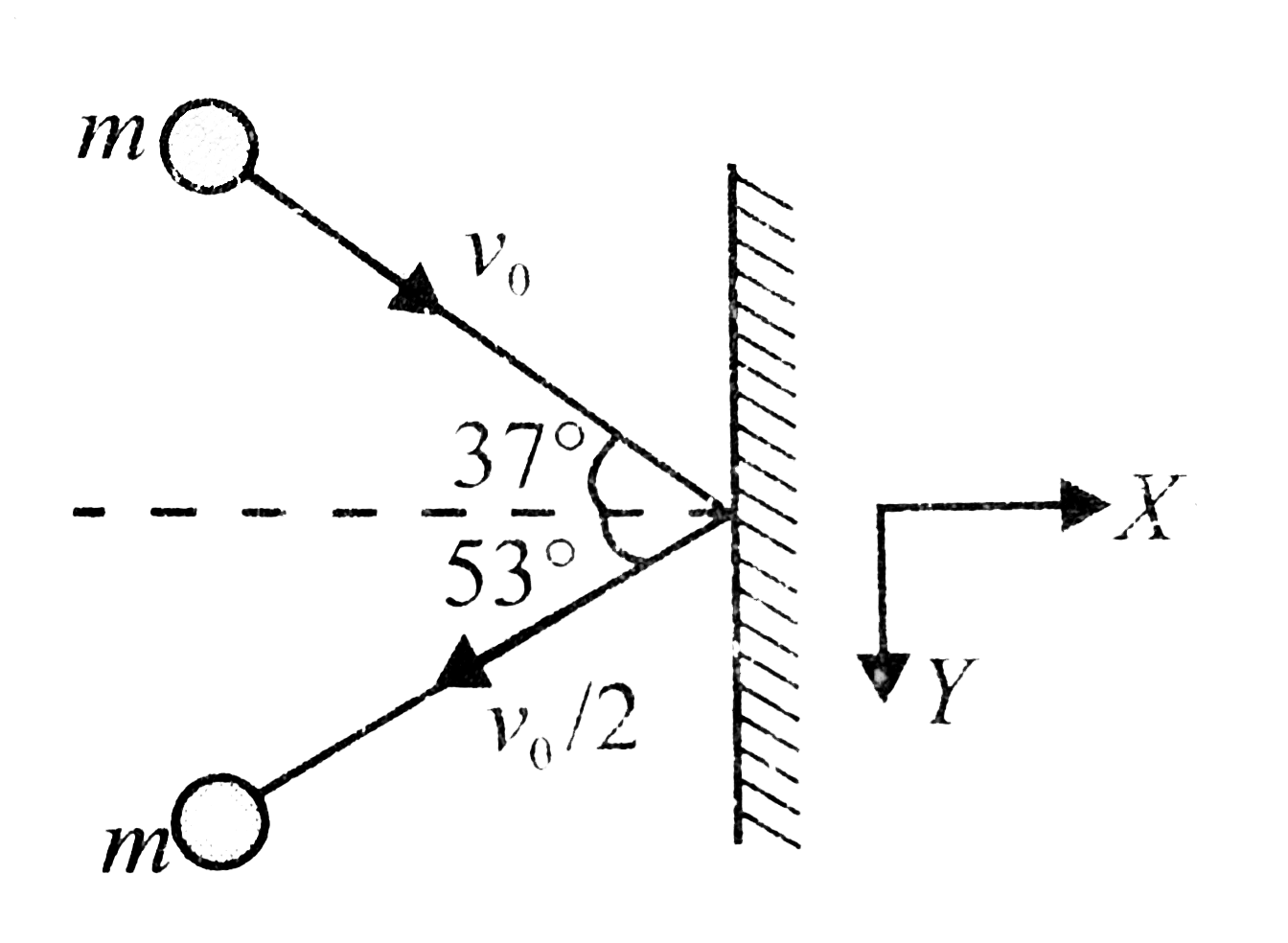 View Solution
View SolutionA railway carriage moves over a straight track with acceleration a. Passenger in the carriage drops a stone. What is the acceleration of the stone w.r.t. the carriage and the earth?
View Solution
