The equation of displacement due to a sound wave is s=s0sin^(2)((wt-kx)). if the bulk modulus of the medium is B, then the equation of pressure variation due to that sound is
Bks0sin(2ωt−2kx)
−Bks0sin(2ωt−2kx)
Bks0cos2(ωt−kx)
−Bks0cos2(ωt−kx)
The correct Answer is:A
To find the equation of pressure variation due to a sound wave given the displacement equation, we can follow these steps:
Step 1: Understand the given displacement equation
The displacement due to a sound wave is given by:
s=s0sin2(ωt−kx)
where:
- s0 is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- t is time,
- x is the position.
Step 2: Differentiate the displacement equation
To find the pressure variation, we need to calculate the spatial derivative of the displacement s:
∂s∂x=∂∂x(s0sin2(ωt−kx))
Using the chain rule, we get:
∂s∂x=s0⋅2sin(ωt−kx)⋅cos(ωt−kx)⋅(−k)
This simplifies to:
∂s∂x=−2ks0sin(ωt−kx)cos(ωt−kx)
Step 3: Use the relationship between pressure and displacement
The pressure variation P in a sound wave is related to the displacement by the equation:
P=−B∂s∂x
where B is the bulk modulus of the medium. Substituting the derivative we found:
P=−B(−2ks0sin(ωt−kx)cos(ωt−kx))
This simplifies to:
P=2Bks0sin(ωt−kx)cos(ωt−kx)
Step 4: Use the double angle identity
Using the double angle identity for sine, sin(2θ)=2sin(θ)cos(θ):
P=Bks0sin(2(ωt−kx))
Final Result
Thus, the equation of pressure variation due to the sound wave is:
P=Bks0sin(2ωt−2kx)
The displacement due to a sound wave is given by:
s=s0sin2(ωt−kx)
where:
- s0 is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- t is time,
- x is the position.
To find the pressure variation, we need to calculate the spatial derivative of the displacement s:
∂s∂x=∂∂x(s0sin2(ωt−kx))
Using the chain rule, we get:
∂s∂x=s0⋅2sin(ωt−kx)⋅cos(ωt−kx)⋅(−k)
This simplifies to:
∂s∂x=−2ks0sin(ωt−kx)cos(ωt−kx)
The pressure variation P in a sound wave is related to the displacement by the equation:
P=−B∂s∂x
where B is the bulk modulus of the medium. Substituting the derivative we found:
P=−B(−2ks0sin(ωt−kx)cos(ωt−kx))
This simplifies to:
P=2Bks0sin(ωt−kx)cos(ωt−kx)
Using the double angle identity for sine, sin(2θ)=2sin(θ)cos(θ):
P=Bks0sin(2(ωt−kx))
Thus, the equation of pressure variation due to the sound wave is:
P=Bks0sin(2ωt−2kx)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Now answer the following :
20 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 89 illustration
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 87
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Knowledge Check
The equation of a wave is given by
y=10sin(2π45t+α)
If the displacement is 5 cm at t = 0, then the total phase at t = 7.5 s isAπ3Bπ2Cπ6Dπ
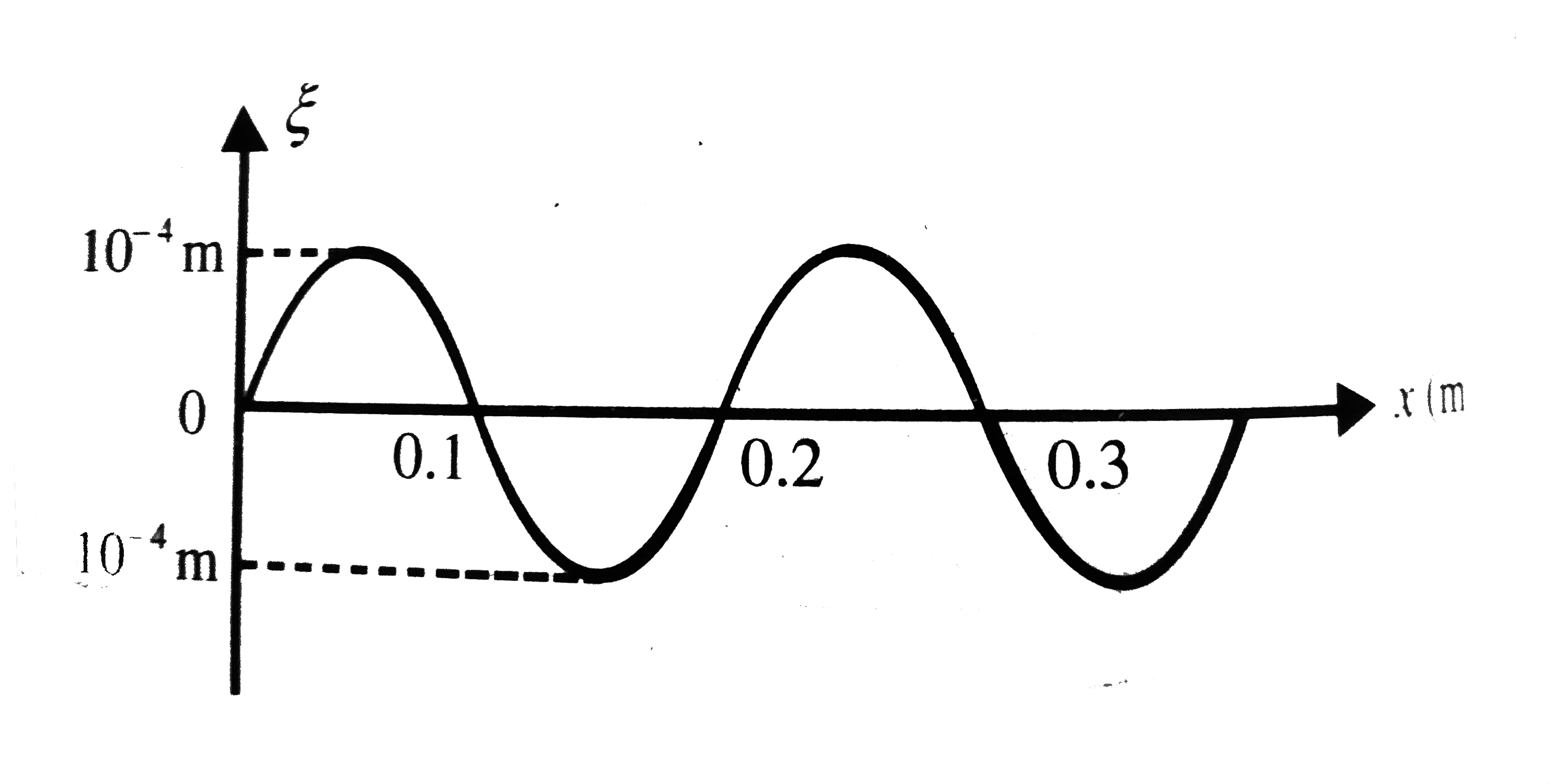
For a sound wave travelling towards +x direction, sinusoidal longitudinal displacement ε at a certain time is given as a function of x (Fig). If bulk modulus of air is B=5×105Nm2, the variation of pressure excess will be
View Solution(a) what is the displacemant amplitude for a sound wave having a frequency of 100Hz and a pressure amplitude of 10 pa? (b) The displacement amplitude of a sound wave of frequency 300Hz is 10−7 m. what is the pressure amplitude of this wave ? speed of sound in airb is 340 ml s and density of a ir is 1.29kg/m3.
View SolutionTwo sound waves one in air and the other in fresh water are equal in intensity.
(a) Find the ratio of pressure amplitude of the wave in water to that of the wave in air.
(b) If the pressure amplitudes of the waves are equal then what will be the ratio of the intensities of the waves.
[Vsound=340m/s in air & density of air =1.25kg/m3,Vsound=1530m/s in water, density of water =1000kg/m3]
View SolutionThe equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
View SolutionThe equation of a longitudinal standing wave due to superposition of the progressive waves producted by two sources of sound is s=−20sin10πxsin100πt where s is the displacement from mean position measured in mm,x is in meters and is in seconds. The specific gravity of the medium is 10−3. Density of water =103kg/m3. Find :
(a) Wavelength, frequency and velocity of the progressive waves.
(b) Bulk modulus of the medium and the pressure amplitude.
(c) Minimum distance between pressure antinode and a displacement anotinode.
(d) Intensity at the displacement nodes.
View SolutionIf a man at the equator would weight (3/5)th of his weight, the angular speed of the earth is:
View SolutionWrite the equation for the fundamental standing sound waves in a tube that is open at both ends. If the tube is 80cm long speed of wave is 330m/s . Represent the amplitude of the wave at an antinode by A .
View Solution
