A particle Is projected at point 'A' with initial velocity 5m/s at an angle θ=37∘ with the vertical y axis. A strong horizontal wind gives the particle a constant horizontal acceleration 6m/s2 in the x direction. If the particle strikes the ground at a point directly under its released position, determine the height 'h' of point A. The downward acceleration is taken as the constant
g=10m/s2(take sin37∘=35,cos37∘=45)
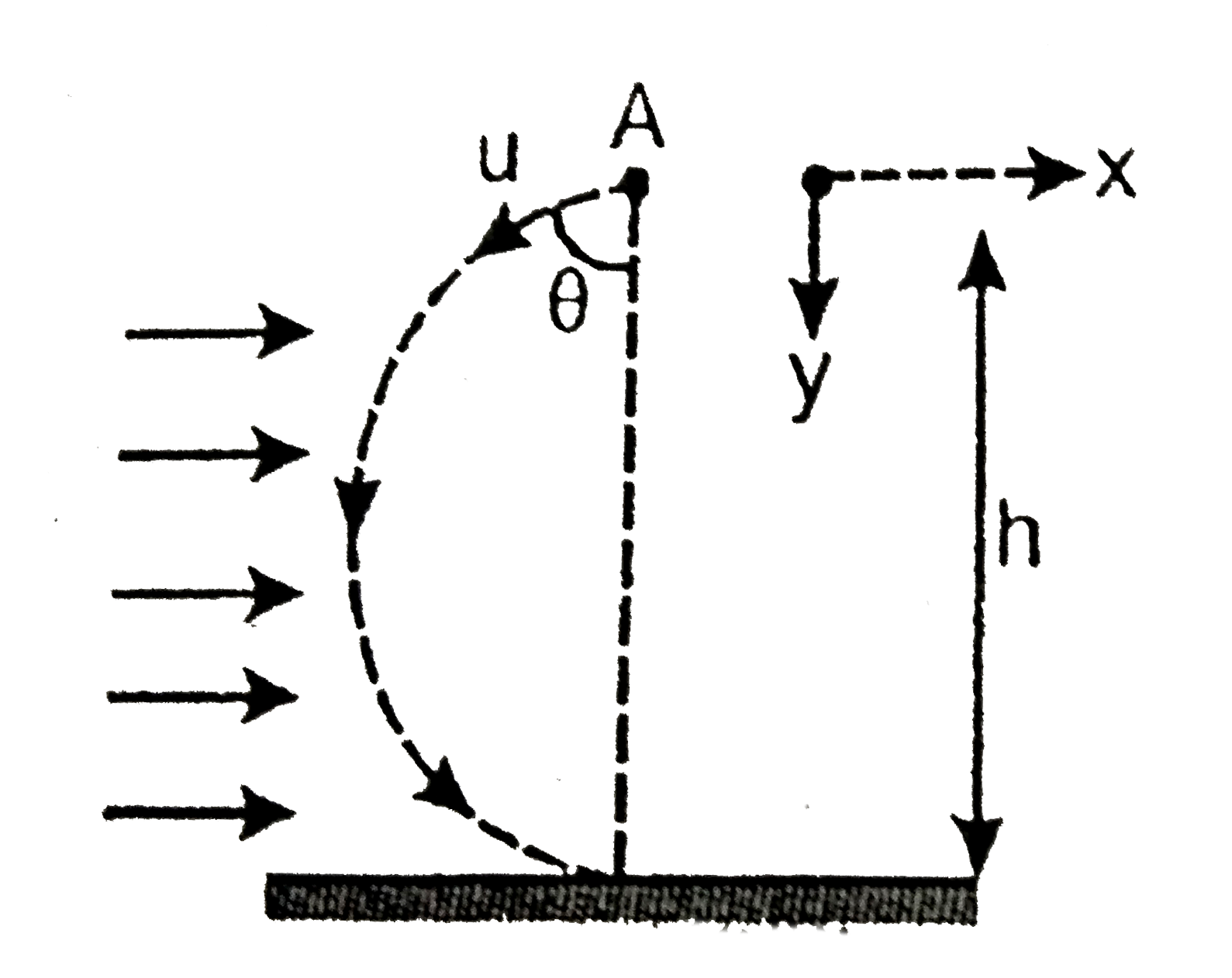
The correct Answer is:9
For A to B
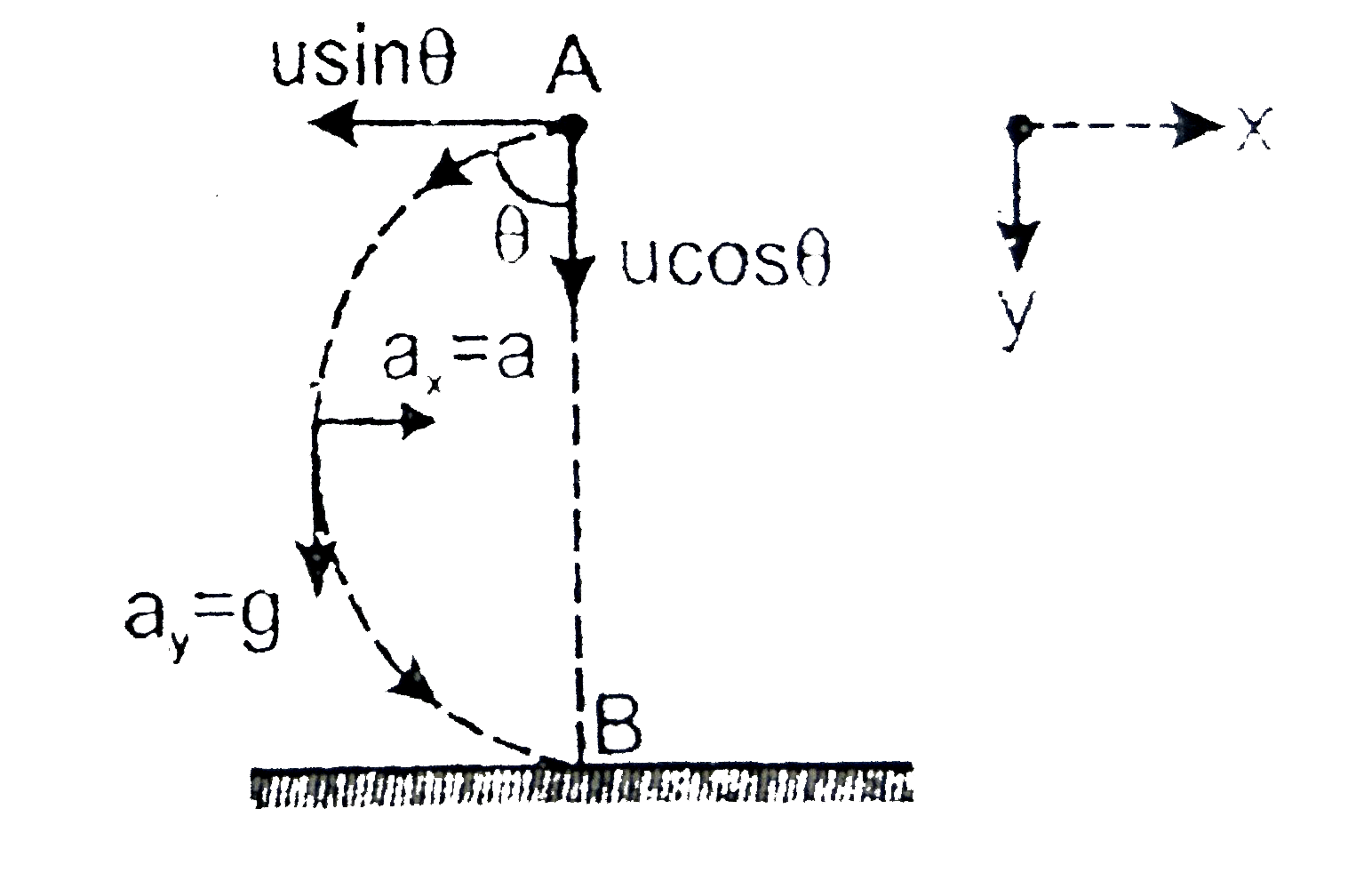
sx=uxt+12axt2
0=−usinθt+12at2
t=2usinθa=2(5)sin37∘6=1 sec.
sy=h=AB=uyt+12ayt2=ucosθt+12gt2
=(5)(45)(1)+12(10)(1)2=9m
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
A particle is ejected from the tube at A with a velocity V at an angle θ with the verticle y-axis at a height h above the ground as shown. A strong horizontal wind gives the particle a constant horizontal acceleration a in the positive x-direction. If the particle strikes the ground at a point directly under its released position and the downward y-acceleration is taken as g then find h.

View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :

View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
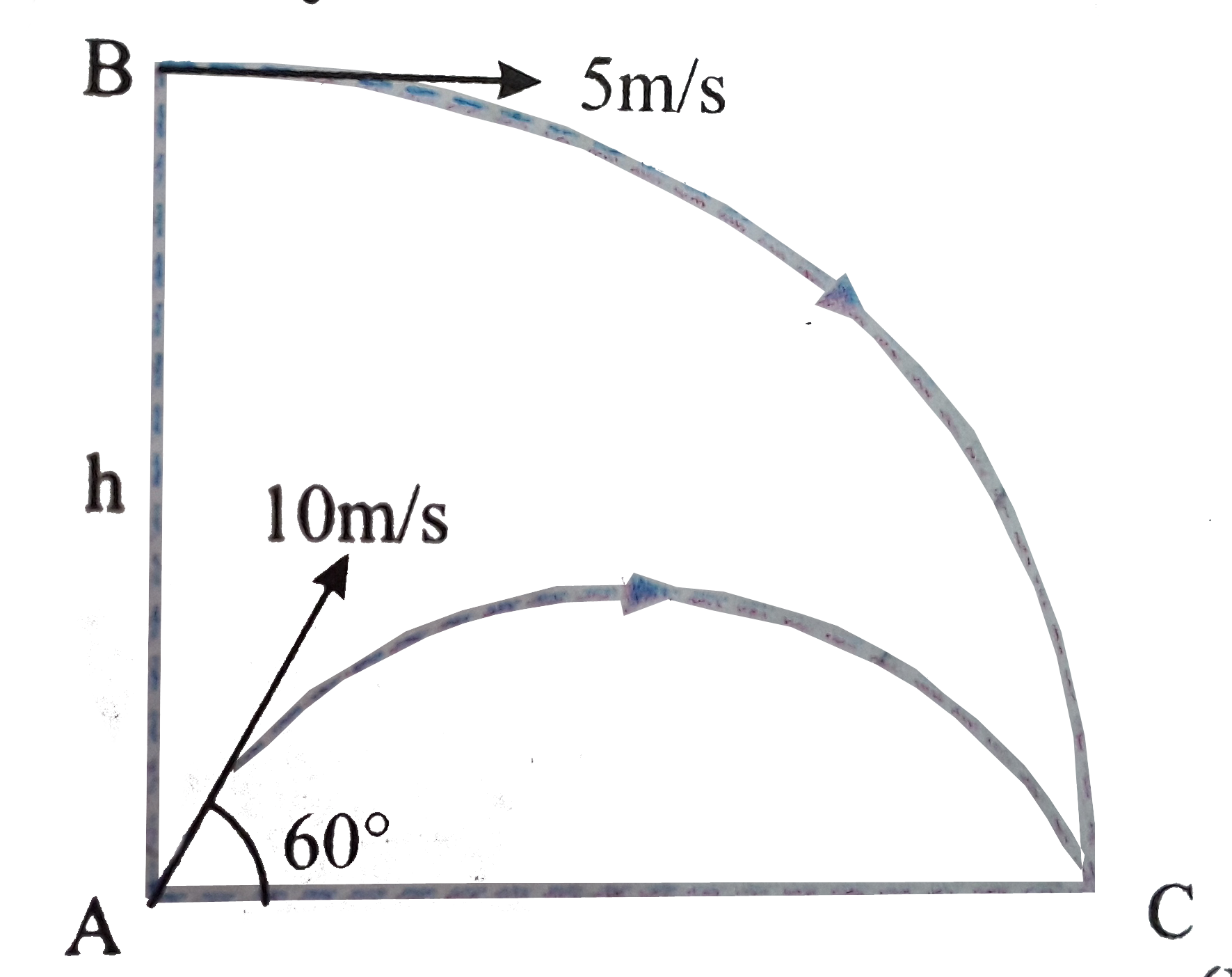
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View Solution

