Question

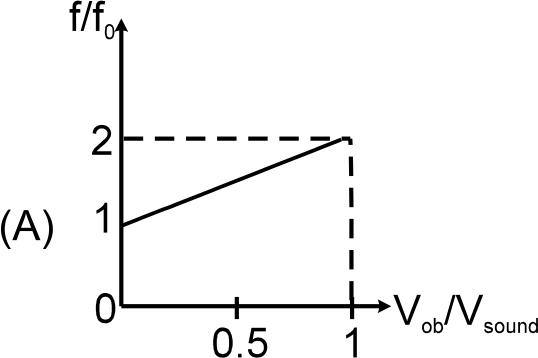
A curve is plotted to represenet the dependence of the ratio of the received frequency $f$ to the frequency $f_0$ emitted by the source on the ratio of the speed of obsever $V_{ob}$ to the speed of sound $V_{sound}$ in a situation in which an observer is moving towards a stationary sound source. The curve is best represnted by :

Options

A.
B.
C.
D.

Explanation

To solve the problem, we need to analyze the relationship between the received frequency $$f$$ and the emitted frequency $$f_0$$ when an observer is moving towards a stationary sound source. We will derive the equation and identify the correct curve representation.

1. Understanding the Doppler Effect:
When an observer moves towards a stationary sound source, the frequency of the sound received by the observer is higher than the frequency emitted by the source. This phenomenon is described by the Doppler effect.

2. Doppler Effect Formula:
The formula for the frequency received by the observer when moving towards a stationary source is given by:
\( f = f_0 \left( \frac{V_{sound} + V_{ob}}{V_{sound}} \right) \)
Here, \( V_{ob} \) is the speed of the observer, and \( V_{sound} \) is the speed of sound.

3. Expressing the Ratio:
We can express the ratio of the received frequency to the emitted frequency:
\( \frac{f}{f_0} = \frac{V_{sound} + V_{ob}}{V_{sound}} \)

4. Simplifying the Expression:
This can be simplified to:
\( \frac{f}{f_0} = 1 + \frac{V_{ob}}{V_{sound}} \)
Let \( x = \frac{V_{ob}}{V_{sound}} \). Therefore, we can rewrite the equation as:
\( \frac{f}{f_0} = 1 + x \)

5. Identifying the Curve:
The equation \( \frac{f}{f_0} = 1 + x \) indicates a linear relationship between \( \frac{f}{f_0} \) (y-axis) and \( \frac{V_{ob}}{V_{sound}} \) (x-axis). The slope of this line is 1 and the y-intercept is also 1.

6. Conclusion:
The best representation of the curve based on the derived equation is a straight line with a slope of 1 and a y-intercept of 1. Therefore, the correct option is the one that represents this linear relationship.