For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
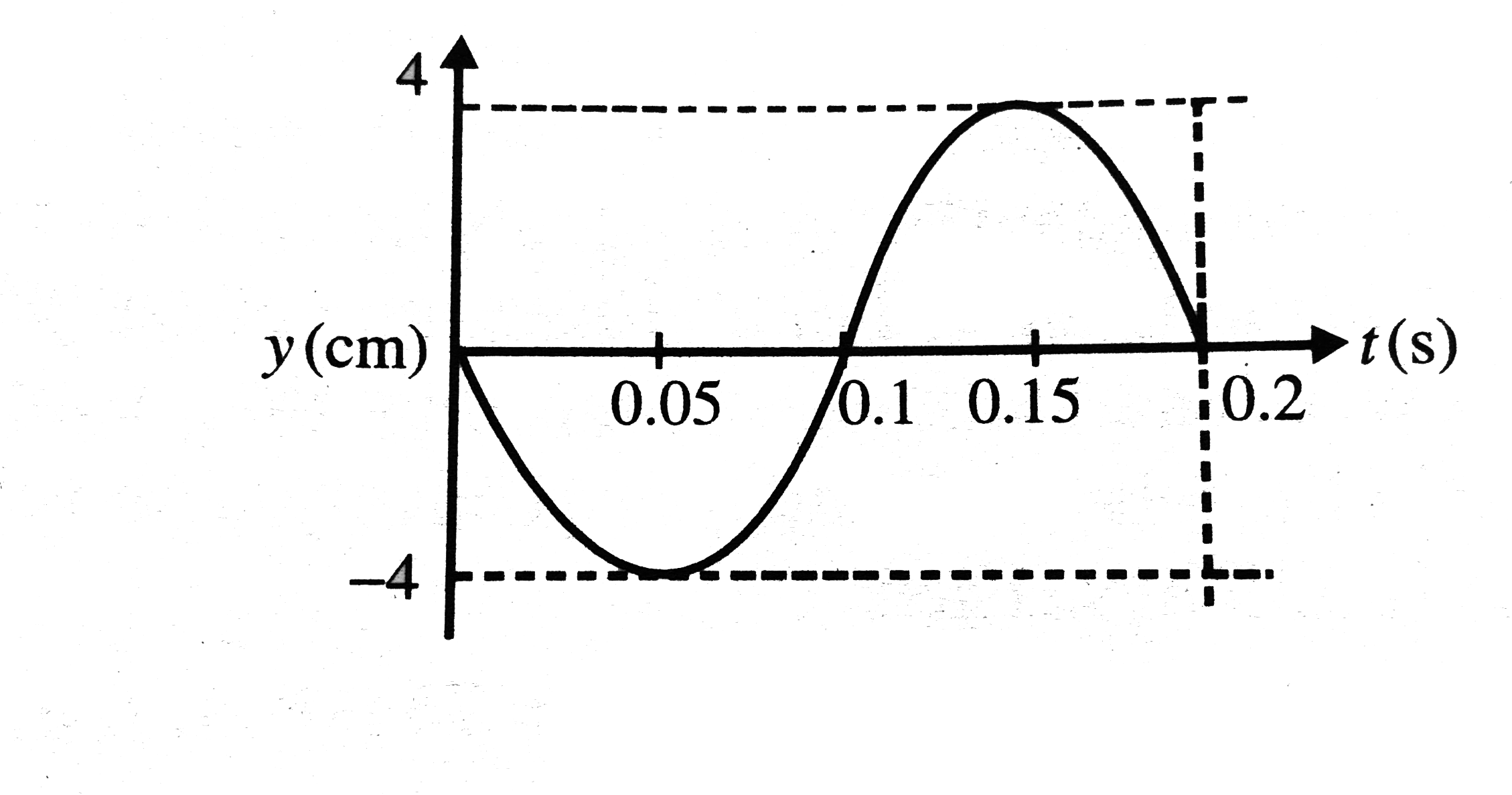
Transverse displacement of the particle at x=0.05 m and t=0.05 s is −2√2 cm
Transverse displacement of the particle at x=0.04 m and t=0.025 s is −2√2 cm
Speed of the travelling waves that interface to produce this standing wave is 2 m/s
The transverse velocity of the string particle at x=115 m and t=0.1 s is 20π cm/s
λ4=0.1⇒λ=0.4m
from graph ⇒ T=0.2 sec and amplitude of standing wave is 2A=4cm
Equation of the standing wave
y(x,t)=−2Acos(2π0.4x)sin(2π0.2t) cm
y(x=0.05,t=0.05=−2√2 cm
y(x=0.05,t=0.25=−2√2cos36∘
speed =λT=2m/sec
Vy=dydt=−2A×2π0.2cos(2πx0.4)cos(2πt0.2)
Vy=(x=115m,t=0.1)=20π cm/sec.
Topper's Solved these Questions
Similar Questions
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
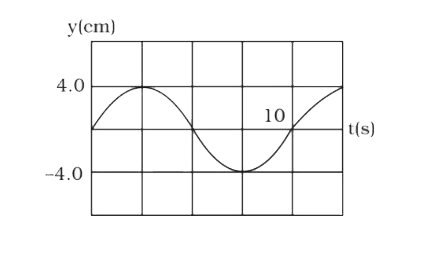
Q. The velocity of propagation of the wave is ?
View SolutionA transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
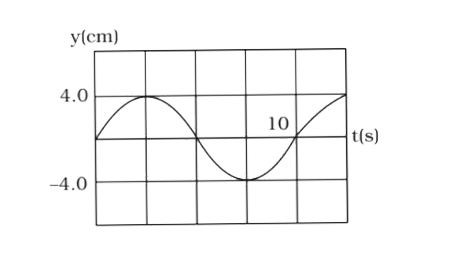
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
View SolutionIn a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m.Then the wave length of the standing wave is
View SolutionThe wave funcation for a travelling wave on a string in given as
y(x,t)=(0.350m)sin(10πt−3πx+π4)
(a) What are the speed and direction of travel of the wave ?
(b) What is the vertical displacement of the string at t=0,x=0.1m ?
View SolutionA wave of length 2m is superposed on its reflected wave to form a stationary wave. A node is located at x = 3m. The next node will be located at x=
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,
View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is y(x,t)=0.5sin(0.025πx)cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :
View Solution
