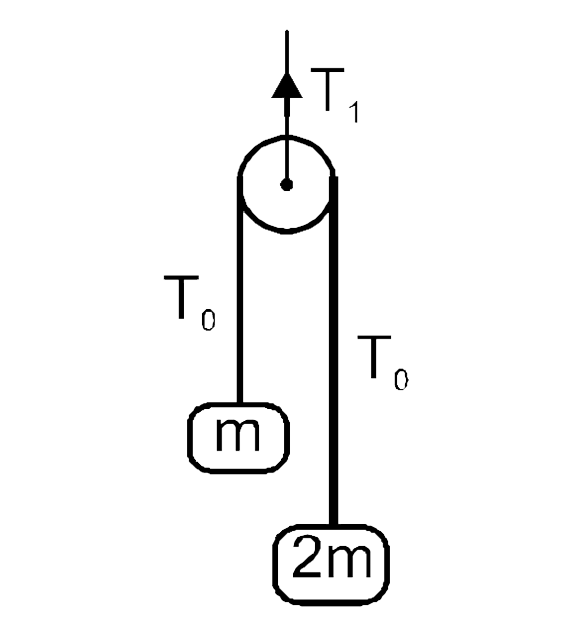
AB wire (length x) is vibrating in its fundamental mode. Wire AB is in resonance with resonance tube in which air column (length x/2) is also vibrating with its fundamental mode. Sound speed is 400 m/sec and linear mass density of AB wire is 10−4 kg/m and g=10 m/sec2, value of mass m =[β(10−1)]kg, then find value of β.Neglect the masses of wires in comparison to block's mass 'm'.
![AB wire (length x) is vibrating in its fundamental mode. Wire AB is in resonance with resonance tube in which air column (length x/2) is also vibrating with its fundamental mode. Sound speed is 400 m/sec and linear mass density of AB wire is 10^-4 kg/m and g=10 m//sec^2, value of mass m =[beta(10^-1)] kg, then find value of beta.Neglect the masses of wires in comparison to block's mass 'm'.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_09_E01_028_Q01.png)
T1=2T0=2[2m(2m)m+2m]g
T1=8m3g=80m3...(i)
In resonance ,
fwire=ftube
(1)V12l1=(1)V24l2
(√T1μ)2(x)=(400)4(x2)
⇒T1=μ(16×104)
From (i), 803m=10−4(16×104)
m=0.6kg.
Topper's Solved these Questions
Similar Questions
A wire of length 40 cm which has a mass of 4 gms oscillates in its second harmonic and sets the air column in the tube to vibrations in its fundamental mode as shown in figure. Assuming speed of sound in air as 340 m/s, find the tension in the wire.

View SolutionA wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View Solution
Knowledge Check
A wire is stretched between two rigid supports vibrates in its fundamental mode with a frequency of 50 Hz. The mass of the wire is 30 g and its linear density is 4×10−2 kg m s−1. The speed of the transverse wave at the string is
A25ms−1B50ms−1C75ms−1D100ms−1
Consider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
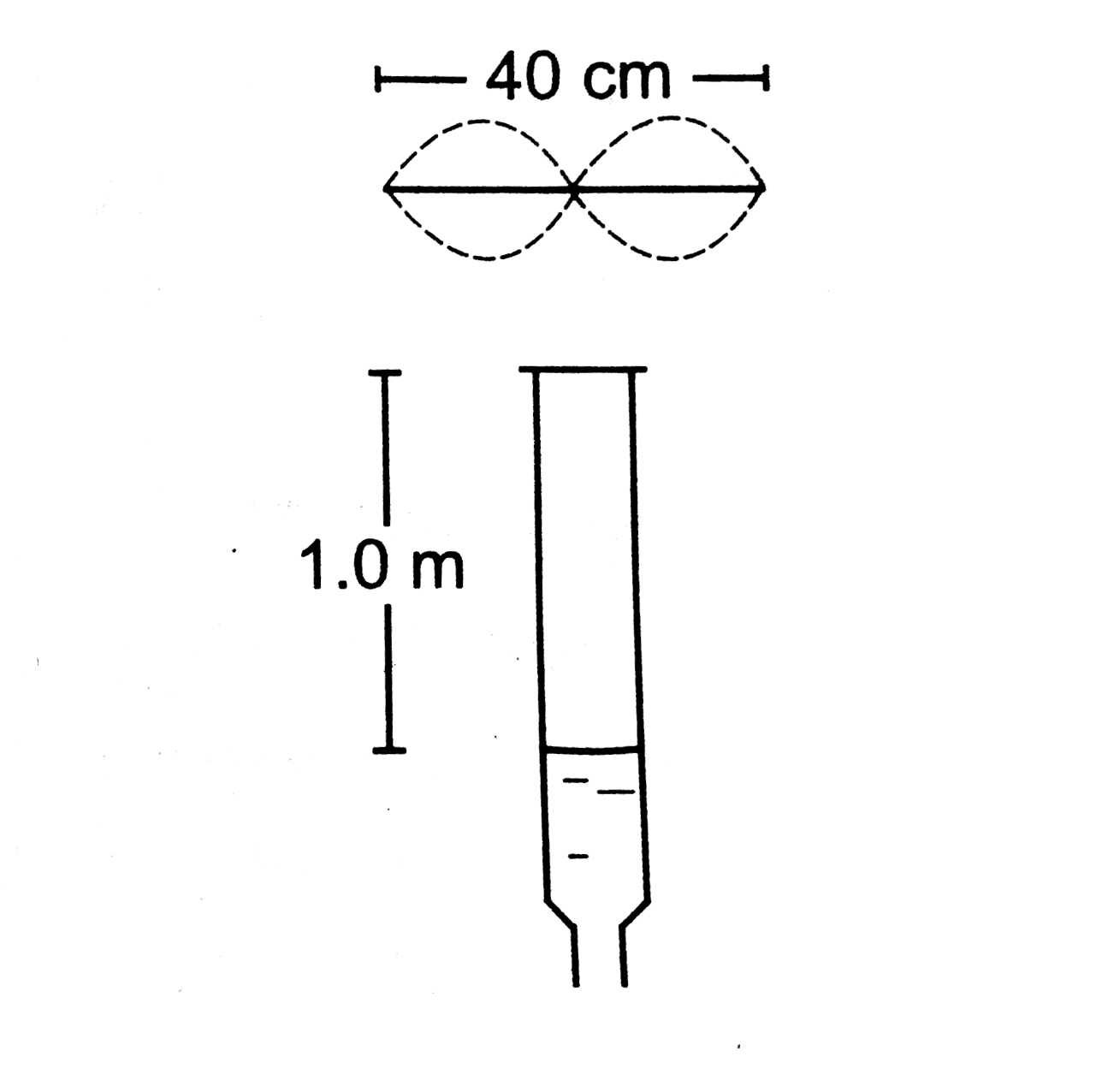 .
.
View SolutionA wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.

View SolutionA wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45Hz. The mass of the wire is 3.5×10−2kg and its linear mass density is 4.0×10−2kgm−1. What is (a) the speed of a transverse wave on the string , and (b) the tension in the string?
View SolutionA wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5×10−2 kg an dits linear mass density is 4×10−2kg/m. What its
(i) the speed of transverse wave in the wire and
(ii) the tension in the wire ?
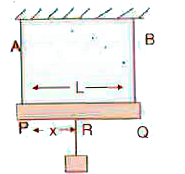
View SolutionA rod PQ of length 'L' is hung from two identical wires A and B. A block of mass 'm' is hung at point R of the rod as shown in figure. The value of 'x' so that the fundamental mode in wire A is in resonance with first overtone of B is
View SolutionA sonometer wire under tension of 64 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of the sonometer wire has a length of 10 cm and mass of 1 g. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved, if the speed of sound in air is 300 m/s.
View SolutionA sonometer wire under tension of 63 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of that sonometer wire has a length of 10 cm and a mass of 1 g. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved if the speed of sound in air is 300 m/s.
View Solution
