Assume Earth's surface is a conductor with a uniform surface charge density σ. It rotates about its axis with angular velocity ω. Suppose the magnetic field due to Sun at Earth at some instant is a uniform field B pointing along earth's axis. Then the emf developed between the pole and equator of earth due to this field is. (Re=radius of earth)
12BωR2e
BωR2e
32BωR2e
zero
To solve the problem, we need to calculate the electromotive force (emf) developed between the pole and the equator of the Earth, which is treated as a conductor with a uniform surface charge density, rotating with angular velocity ω in the presence of a uniform magnetic field B pointing along the Earth's axis.
1. Understanding the Setup:
- The Earth is modeled as a conductor with a uniform surface charge density σ.
- It rotates about its axis with angular velocity ω.
- A uniform magnetic field B from the Sun is present, pointing along the Earth's axis.
2. Using Faraday's Law of Electromagnetic Induction:
- According to Faraday's law, the induced emf E in a loop is given by:
E=−dΦBdt
- Where ΦB is the magnetic flux through the loop.
3. Calculating the Area:
- The area A of the circular path traced by a point on the surface of the Earth at the equator is:
A=πR2e
- Here, Re is the radius of the Earth.
4. Determining the Change in Flux:
- The change in magnetic flux ΦB can be expressed as:
ΦB=B⋅A=B⋅πR2e
5. Finding the Rate of Change of Flux:
- Since the Earth is rotating, the effective area swept out per unit time at the equator is:
dAdt=R2e⋅ω
- Thus, the induced emf can be calculated as:
E=B⋅R2e⋅ω
6. Considering the Poles:
- At the poles, the velocity due to rotation is zero, so the emf at the pole is:
Epole=0
7. Calculating the Total Induced EMF:
- The emf developed between the pole and the equator can be given by:
Etotal=Eequator−Epole=BR2eω−0
- However, since we are looking for the emf between the pole and the equator, we take the average:
E=12BR2eω
8. Final Result:
- Therefore, the emf developed between the pole and the equator of the Earth is:
E=12BR2eω
- The Earth is modeled as a conductor with a uniform surface charge density σ.
- It rotates about its axis with angular velocity ω.
- A uniform magnetic field B from the Sun is present, pointing along the Earth's axis.
- According to Faraday's law, the induced emf E in a loop is given by:
E=−dΦBdt
- Where ΦB is the magnetic flux through the loop.
- The area A of the circular path traced by a point on the surface of the Earth at the equator is:
A=πR2e
- Here, Re is the radius of the Earth.
- The change in magnetic flux ΦB can be expressed as:
ΦB=B⋅A=B⋅πR2e
- Since the Earth is rotating, the effective area swept out per unit time at the equator is:
dAdt=R2e⋅ω
- Thus, the induced emf can be calculated as:
E=B⋅R2e⋅ω
- At the poles, the velocity due to rotation is zero, so the emf at the pole is:
Epole=0
- The emf developed between the pole and the equator can be given by:
Etotal=Eequator−Epole=BR2eω−0
- However, since we are looking for the emf between the pole and the equator, we take the average:
E=12BR2eω
- Therefore, the emf developed between the pole and the equator of the Earth is:
E=12BR2eω
Topper's Solved these Questions
Similar Questions
A long cylinder of radius a carrying a uniform surface charge rotates about its axis with an angular velocity ω. Find the magnetic field energy per unit length of the cylinder if the linear charge density equals λ and μ=1.
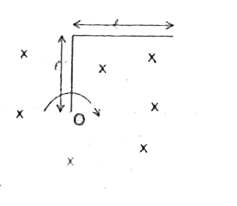
View SolutionFor the L shaped conductor in a uniform magnetic field B shown in figure the emf across its ends when it rotates with angular velocity ω about an axis through one its ends O and normal to its plane will be
View Solution
Knowledge Check
A metal conductor of length 1m rotates vertically about one of its ends at angular velocity 5 radians per second. If the horizontal component of earth's magnetic field is 0.2×10−4T, then the emf developed between the two ends of hte conductor is
A5μVB5mVC50μVD50mVA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
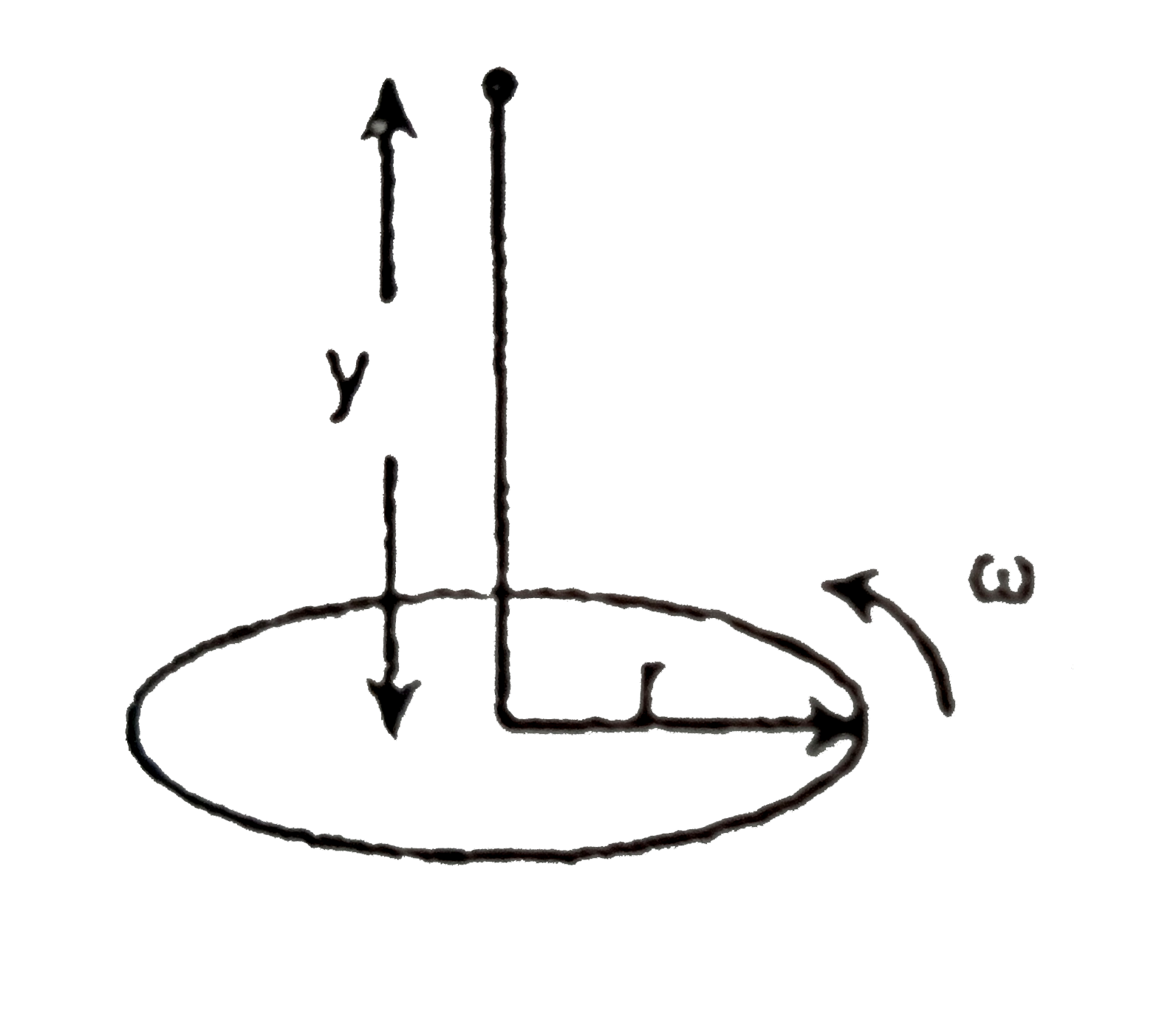
Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View SolutionA long, hollow insulating cylinder of radius R and negligible thickness has a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω. Choose the correct option(s):
View SolutionThe mean radius of earth is R, its angular speed on its own axis is w and the acceleration due to gravity at earth's surface is g. What will be the cube of radius of the orbit of a geostationary satellite
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
