Consider a series LCR circuit connected to an AC supply of 220V. If voltage drop across resistance R is VR, voltage drop across capacitor is Vc=2VR and that across inudctor coil is VL=2VR then choose correct alternative(s)
VR=220√2
Power factor of circuit is 1√2
VR=156V
Phase difference between current and source voltage is π4
To solve the problem, we need to analyze the voltage drops in a series LCR circuit connected to an AC supply. Given the following:
1. Voltage drop across resistance R is VR.
2. Voltage drop across the capacitor C is VC=2VR.
3. Voltage drop across the inductor L is VL=2VR.
4. The total supply voltage is Vsupply=220V.
Step 1: Write the expressions for the voltage drops.
- We have:
VR=VR(acrossR)
VC=2VR(acrossC)
VL=2VR(acrossL)
Step 2: Determine the total voltage in the circuit.
- In an LCR circuit, the total voltage Vsupply can be expressed in terms of the voltage drops across the components:
Vsupply=√V2R+(VL−VC)2
Step 3: Substitute the values of VC and VL.
- Substitute VC and VL into the equation:
Vsupply=√V2R+(2VR−2VR)2
Vsupply=√V2R+0=VR
Step 4: Set the equation equal to the supply voltage.
- Since Vsupply=220V, we have:
VR=220V
Step 5: Calculate the voltage drops across C and L.
- Now, calculate VC and VL:
VC=2VR=2×220=440V
VL=2VR=2×220=440V
Step 6: Check the phase relationship.
- The voltage across the capacitor leads the current by π2 and the voltage across the inductor lags the current by π2. This means that:
- The total voltage across C and L cancels out, leading to a net effect on the circuit.
Step 7: Calculate the power factor.
- The power factor PF is given by:
PF=cos(ϕ)
where ϕ is the phase angle. Since VC and VL are equal and opposite, the net voltage across them is zero, leading to a phase angle of π4:
PF=cos(45∘)=1√2
Conclusion:
- The voltage drop across the resistance VR is 156V.
- The phase difference between the current and the source voltage is π4.
2. Voltage drop across the capacitor C is VC=2VR.
3. Voltage drop across the inductor L is VL=2VR.
4. The total supply voltage is Vsupply=220V.
- We have:
VR=VR(acrossR)
VC=2VR(acrossC)
VL=2VR(acrossL)
- In an LCR circuit, the total voltage Vsupply can be expressed in terms of the voltage drops across the components:
Vsupply=√V2R+(VL−VC)2
- Substitute VC and VL into the equation:
Vsupply=√V2R+(2VR−2VR)2
Vsupply=√V2R+0=VR
- Since Vsupply=220V, we have:
VR=220V
- Now, calculate VC and VL:
VC=2VR=2×220=440V
VL=2VR=2×220=440V
- The voltage across the capacitor leads the current by π2 and the voltage across the inductor lags the current by π2. This means that:
- The total voltage across C and L cancels out, leading to a net effect on the circuit.
- The power factor PF is given by:
PF=cos(ϕ)
where ϕ is the phase angle. Since VC and VL are equal and opposite, the net voltage across them is zero, leading to a phase angle of π4:
PF=cos(45∘)=1√2
- The voltage drop across the resistance VR is 156V.
- The phase difference between the current and the source voltage is π4.
Topper's Solved these Questions
Similar Questions
In series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionIn series L−C−R circuit, voltge drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then,
View SolutionIn a series LCR circuit, the the rms voltage supply is 170 V. If VR,VLandVC represent the rms voltage drop across resistor , inductor and capacitor, then
View SolutionIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
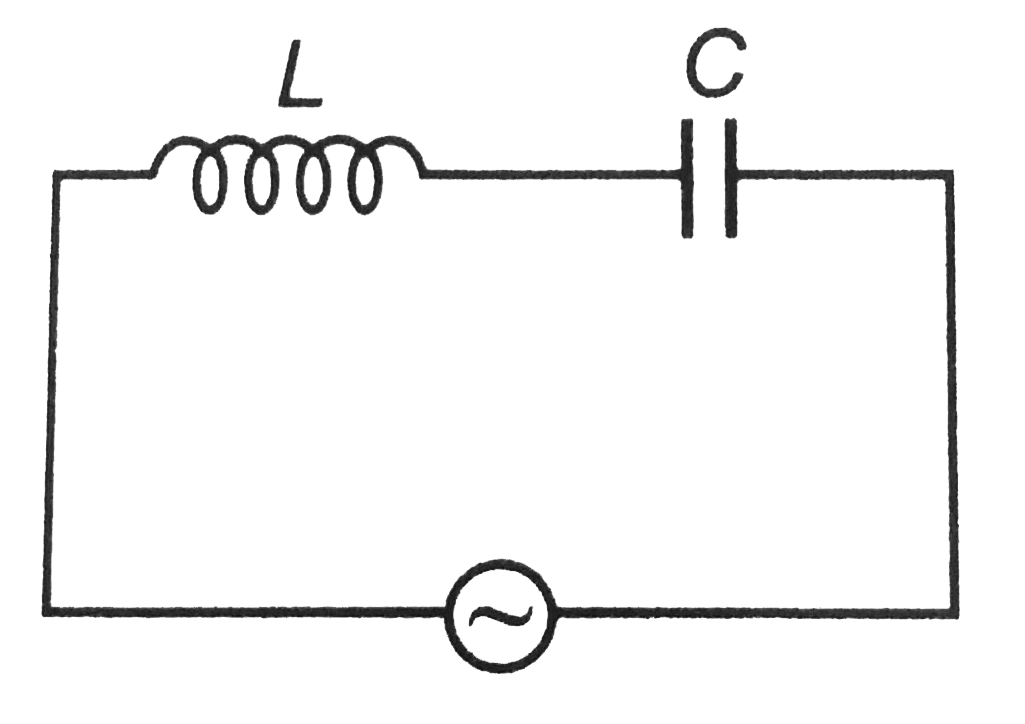 .
.
View SolutionAn LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
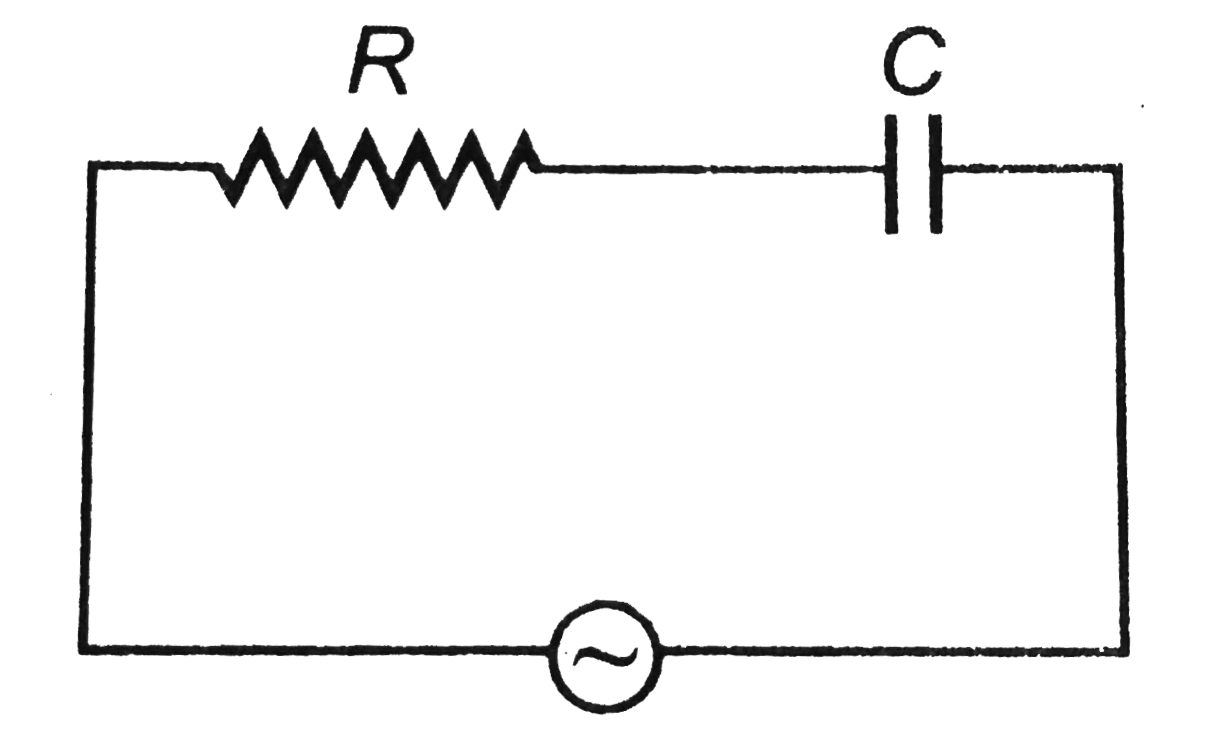
View SolutionA 50HzAC source of 20V is connected across R and C as shown in figure.
The voltage across R is 12V. The voltage across C is
View SolutionFind the voltage drop across a capacitor connected with a resistance and a battery of 60 V in series after a long time.
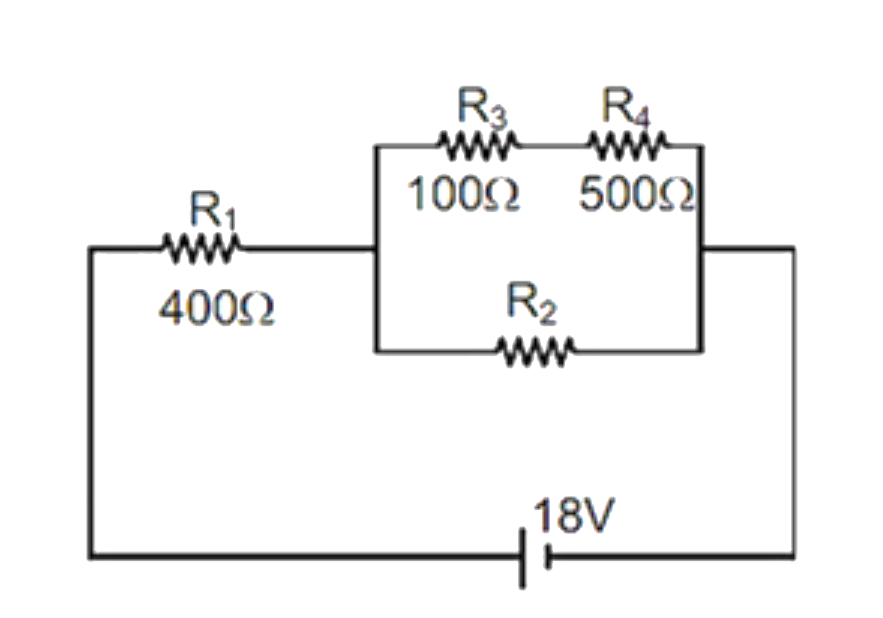
View SolutionIf the voltage across 500Ω is 5 V. then R2 is
View SolutionA 50HzAC source of 20V is connected across R and C as shown in figureure.

The voltage across R is 12V. The voltage across C is
View SolutionA resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View Solution