A particle of mass 100 g, is made to describe a vertical circle of radius 1 m. Its instantaneous speed is 1ms−1 when the string makes an sngle of 30∘ with the vertical Find the tension in the string at this position. Can the particle complete its circular path? (g=10ms−2)
To solve the problem step by step, we will first determine the tension in the string when the particle is at an angle of 30∘ with the vertical and then check if the particle can complete the circular path.
Step 1: Identify the given values
- Mass of the particle, m=100g=0.1kg
- Radius of the circle, r=1m
- Instantaneous speed, v=1m/s
- Angle with the vertical, θ=30∘
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the components of forces acting on the particle
At the position where the string makes an angle of 30∘ with the vertical, two forces act on the particle:
1. The tension T in the string.
2. The weight mg of the particle, which can be resolved into two components:
- mgcosθ (along the direction of the string)
- mgsinθ (perpendicular to the direction of the string)
Step 3: Write the equation for circular motion
For the particle to maintain circular motion, the net force acting towards the center of the circle must equal the centripetal force required for circular motion. The centripetal force is given by:
Fc=mv2r
The net force towards the center is the difference between the tension in the string and the component of the weight acting along the radius:
T−mgcosθ=mv2r
Step 4: Substitute the known values into the equation
Substituting the values into the equation:
T−(0.1⋅10⋅cos30∘)=0.1⋅(1)21
Calculating mgcos30∘:
mgcos30∘=0.1⋅10⋅√32=0.1⋅10⋅0.866=0.866N
Now substituting this into the equation:
T−0.866=0.1
T=0.1+0.866=0.966N
Step 5: Determine if the particle can complete the circular path
To check if the particle can complete the circular path, we need to find the minimum speed required at the top of the circle. The minimum speed vmin at the top of the circle is given by:
vmin=√gr
Substituting the values:
vmin=√10⋅1=√10≈3.16m/s
Step 6: Compare the speeds
The instantaneous speed at the angle of 30∘ is 1m/s, which is less than the minimum speed of 3.16m/s. Therefore, the particle cannot complete the circular path.
Final Answers
- The tension in the string at the position where the angle is 30∘ is T=0.966N.
- The particle cannot complete the circular path.
- Mass of the particle, m=100g=0.1kg
- Radius of the circle, r=1m
- Instantaneous speed, v=1m/s
- Angle with the vertical, θ=30∘
- Acceleration due to gravity, g=10m/s2
At the position where the string makes an angle of 30∘ with the vertical, two forces act on the particle:
1. The tension T in the string.
2. The weight mg of the particle, which can be resolved into two components:
- mgcosθ (along the direction of the string)
- mgsinθ (perpendicular to the direction of the string)
For the particle to maintain circular motion, the net force acting towards the center of the circle must equal the centripetal force required for circular motion. The centripetal force is given by:
Fc=mv2r
T−mgcosθ=mv2r
Substituting the values into the equation:
T−(0.1⋅10⋅cos30∘)=0.1⋅(1)21
Calculating mgcos30∘:
mgcos30∘=0.1⋅10⋅√32=0.1⋅10⋅0.866=0.866N
Now substituting this into the equation:
T−0.866=0.1
T=0.1+0.866=0.966N
To check if the particle can complete the circular path, we need to find the minimum speed required at the top of the circle. The minimum speed vmin at the top of the circle is given by:
vmin=√gr
Substituting the values:
vmin=√10⋅1=√10≈3.16m/s
The instantaneous speed at the angle of 30∘ is 1m/s, which is less than the minimum speed of 3.16m/s. Therefore, the particle cannot complete the circular path.
- The tension in the string at the position where the angle is 30∘ is T=0.966N.
- The particle cannot complete the circular path.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA small stone of mass 100 g in rotated I a verticlal circle of radius 40 cm. What is the minimum speed needed at the lowest point for looping the loop? Also find the tension in the string at this point (g=10ms−2).
View SolutionA ball of mass 0.6kg attached to a light inextensible string rotates in a vertical circle of radius 0.75m such that it has speed of 5ms−1 when the string is horizontal. Tension in the string when it is horizontal on other side is (g=10ms−2).
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionCalculate the tension in the string shown in the figure. All the surfaces are frictionless. (Take g=10/ms−1)
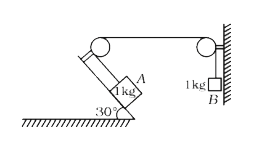
View SolutionA particle is moving on a circular track of radius 30 cm with a constant speed of 6ms−1. Its acceleration is
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution
