Considering equal mases, get the expressions for the velocities of bodies after the collision.
To derive the expressions for the velocities of two bodies after a collision, we will consider two bodies with equal masses undergoing a perfectly elastic collision. Let's denote the masses as m1 and m2, and their initial velocities as u1 and u2. After the collision, we denote their final velocities as V1 and V2.
1. Define the Initial Conditions:
- Let m1=m and m2=m (since the masses are equal).
- Initial velocities are u1 for mass m1 and u2 for mass m2.
2. Use Conservation of Momentum:
- The total momentum before the collision is equal to the total momentum after the collision.
- Mathematically, this is expressed as:
mu1+mu2=mV1+mV2
- Simplifying, we get:
u1+u2=V1+V2(Equation 1)
3. Use Conservation of Kinetic Energy:
- For a perfectly elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
- This can be expressed as:
12mu21+12mu22=12mV21+12mV22
- Simplifying, we have:
u21+u22=V21+V22(Equation 2)
4. Substituting Equal Masses:
- Since m1=m2=m, we can substitute m into our equations.
5. Solving the Equations:
- From Equation 1, we can express V2 in terms of V1:
V2=u1+u2−V1(Equation 3)
- Substitute V2 from Equation 3 into Equation 2:
u21+u22=V21+(u1+u2−V1)2
- Expanding the right-hand side:
u21+u22=V21+(u21+u22+2u1u2−2u1V1−2u2V1)
- Simplifying gives:
0=2u1u2−2u1V1−2u2V1
- Factoring out 2:
0=u1u2−(u1+u2)V1
- Rearranging gives:
V1=u1u2u1+u2(Equation 4)
6. Finding Final Velocities:
- Using the derived equations, we can find V1 and V2:
- Since m1=m2, we find:
V1=u2(final velocity of mass 1)
V2=u1(final velocity of mass 2)
Conclusion:
The final velocities of the two bodies after an elastic collision with equal masses are:
- V1=u2
- V2=u1
This indicates that the velocities of the two bodies are interchanged after the collision.
- Let m1=m and m2=m (since the masses are equal).
- Initial velocities are u1 for mass m1 and u2 for mass m2.
- The total momentum before the collision is equal to the total momentum after the collision.
- Mathematically, this is expressed as:
mu1+mu2=mV1+mV2
- Simplifying, we get:
u1+u2=V1+V2(Equation 1)
- For a perfectly elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
- This can be expressed as:
12mu21+12mu22=12mV21+12mV22
- Simplifying, we have:
u21+u22=V21+V22(Equation 2)
- Since m1=m2=m, we can substitute m into our equations.
- From Equation 1, we can express V2 in terms of V1:
V2=u1+u2−V1(Equation 3)
- Substitute V2 from Equation 3 into Equation 2:
u21+u22=V21+(u1+u2−V1)2
- Expanding the right-hand side:
u21+u22=V21+(u21+u22+2u1u2−2u1V1−2u2V1)
- Simplifying gives:
0=2u1u2−2u1V1−2u2V1
- Factoring out 2:
0=u1u2−(u1+u2)V1
- Rearranging gives:
V1=u1u2u1+u2(Equation 4)
- Using the derived equations, we can find V1 and V2:
- Since m1=m2, we find:
V1=u2(final velocity of mass 1)
V2=u1(final velocity of mass 2)
The final velocities of the two bodies after an elastic collision with equal masses are:
- V1=u2
- V2=u1
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Knowledge Check
A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘Consider the following statements A and B. Identify the correct choice in the given answers
A. In a one dimensional perfectly elastic collision between two moving bodies of equal masses the bodies merely exchange their velocities after collision.
B. If a lighter body at rest suffers perfectly elastic collision with a very heavy body moving with a certain velocity, then after collision both travel with same velocity.AA and B are correctBBoth A and B are wrongCA is correct, B is wrongDA is wrong, B is correct
Two indentical balls A and B moving with velocities uA and uB In the same direction collide. Coefficient of restitution is e.
(a) Deduce expression for velocities of the balls after the collision.
(b) If collision is perfectly elastic, what do you observe?
View SolutionA body of mass m moving with a constant velocity collides head on with another stationary body of same mass if the coefficient of restitution between the bodies is 12 then ratio of velocities of two bodies after collision with be
View SolutionIn figure, determine the character of the collision. The masses of the blocks, and the velocities before and after are given. The collision is
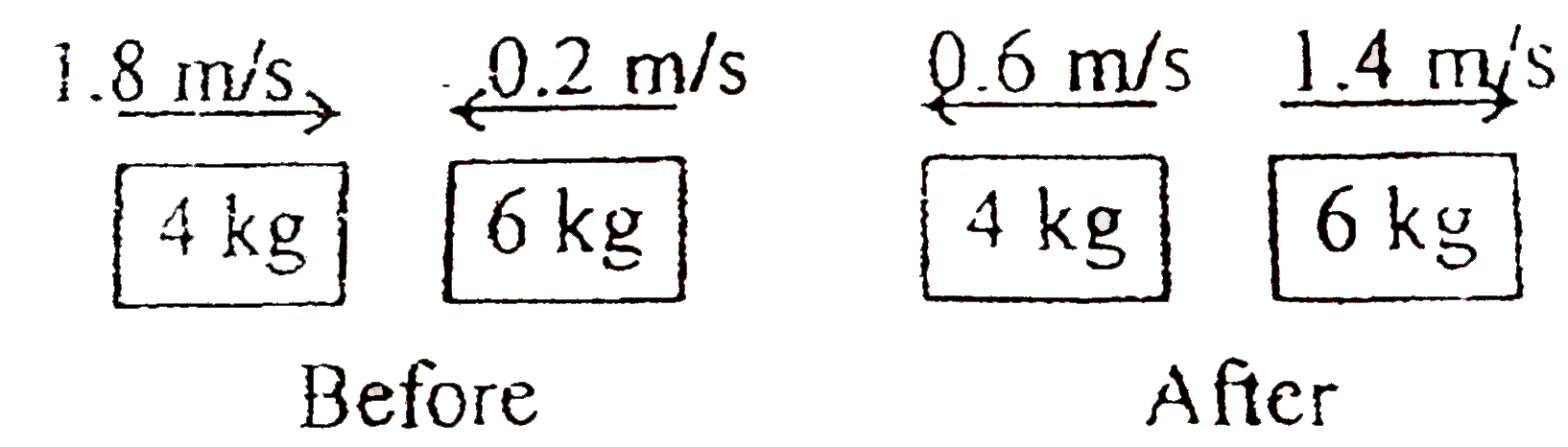
View SolutionDerive an expression for the escape velocity of a body from any planet.
View SolutionA body of rest mass m0 collides perfectly inelastically at a speed of 0.8c with another body of equal rest mass kept at rest . Calculate the common speed of the bodies after the collision and the rest mass of the combined body .
View SolutionConsider the elastic collision f two bodies A and B of equal mass. Initially B is at rest and A moves with velocity v. After the collision -
View Solution
