A particle is moving along x-axis under the action of force, F which varies with its position as F∝14√x. Find the variation of power due to this fore with x.
F∝x−1/2∴a=Kx−1/2
aorvdvdx=kx−1/2 ltbr"gt ∫vdv=k∫x−1/2dx
Find v. P=Fv
P∝v√x
F∝x1/2
a∝−1/2
a=kx−1/2 (k is a proporationality constant)
dvdt=dxdtdvdx=kx−1/2
vdvdx=kx−1/2
∫vdv=k∫x−1/2dx
v22=kx1/21/2
v2∝x1/2
v∝x1/4
P=Fv
P∝x1/4√4
P∝x−1/4
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)60videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)45videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION2videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A particle is moving along x-axis under the action of a force F, which varies with its position (x)asF∝1√x.Find the variation of power due to this force with x.
View SolutionA particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
View SolutionA particle starts moving from rest along y axis and a variable force F acts on it such that F∞y−15 (y>0). The variation of power P of this force with y is given as
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View SolutionA 4kg particle is moving along the x- axis under the action of the force F=−(π216)xN At t=2sec the particle passes through the origin and t=10sec, the speed is 4√2m/s The amplitude of the motion is
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
 View Solution
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then
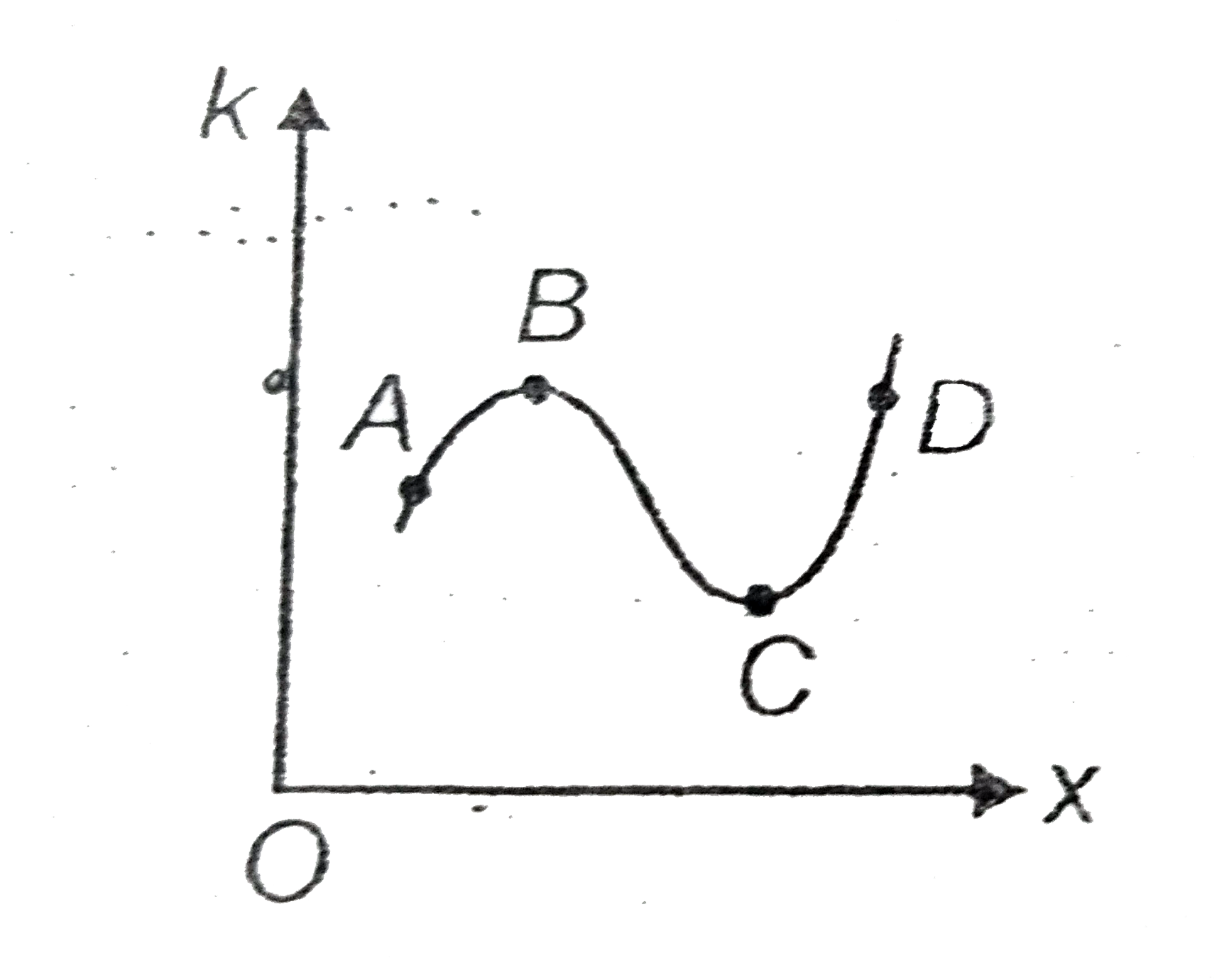 View Solution
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View Solution
