Two cylindrical vessels of equal cross-sectional area A contain water up to heights h1 and h2. The vessels are interconnected so that the levels in them are equal.Calculate the work done by the force of gravity during the process. The density of water is p.
(h1−h2)gρ
(h1−h2)gAρ
12(h1−h2)2gAρ
14(h1−h2)gAp
The correct Answer is:D


If h is the common height when they are connected, by conservation of mass
ρA1h1ρA2h2=ρh(A1+A2)
h=(h1+h2)2
As (h12) and (h22) are heights of initial centre of gravity of liquid in two vassels, the initial potential energy of the system
Ui=(h1Aρ)g(h1)2+(h2Aρ)h22=ρgA(h21+h22)2
When vessels are connected the height of centre of gravity of liquid in each vassel will be b2,
i.e. (h1+h2)4 [as h=(h1+h2)2)]
UF=[(h1+h2)2Aρ]g(h1+h24)
=Aρg[(h1+h2)24
W=Ui−Uf=14ρgA[2(h21+h22)−(h1+h2)2]
=14ρgA(h1≈h2)2
Similar Questions
Two cyllindrical vessels of equal cross sectional ara A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is ρ
View SolutionTwo identical cylindrical vessel with their bases at the same level each contain a liquid of density ρ. The height of the liquid in one vessel is h1 and in the other is h2 the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
View SolutionMercury of density ρm is poured into cylinderical communicating vessels of cross-sectional area 2A and A respectively. A solid iron cube of volume V0 and relative density 2 is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then, water is poured into the broader vessel until the mercury reaches the previous level in it. Find the height of water column if it does not submerge the block.
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionWater at 50∘C is filled in a closed cylindrical vessel of height 10cm and cross sectional area 10cm2 The walls of the vessel are adiabatic but the flat parts are made of 1−mm thick aluminium (K=200Js−2m−1C−1 . Assume that the outside temperature is 20∘C . The density of water is 1000kgm−3 and the specify heat capacity of water =4200Jkg−1C−1 .Estimate the time taken for the temperature to fall by 1.0∘C . Make any simplifying assumption you need but specify them.
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is
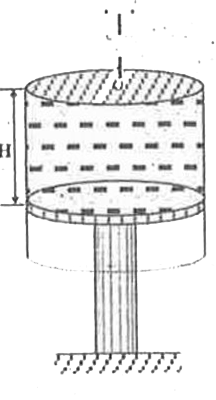
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
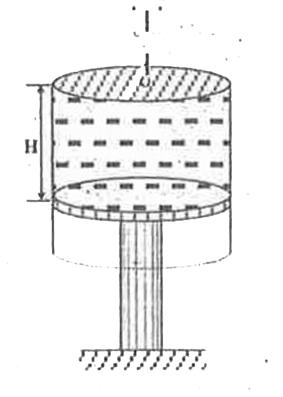
View SolutionA cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the time required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View SolutionA cylindrical vessel open at the top is 20cm high and 10cm in diameter. A circular hole of cross-sectional area 1cm2 is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate of 102cm3/s. The height of water in the vessel under steady state is (Take g=10m/s2).
View SolutionIn a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

View Solution

