A cylindrical vessel open at the top is 20cm high and 10cm in diameter. A circular hole of cross-sectional area 1cm2 is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate of 102cm3/s. The height of water in the vessel under steady state is (Take g=10m/s2).
20cm
15cm
10cm
5cm
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a cylindrical vessel that is 20 cm high and 10 cm in diameter. There is a hole at the bottom with a cross-sectional area of 1 cm², and water is entering the vessel at a rate of 100 cm³/s. We need to find the steady-state height of the water in the vessel.
Step 2: Identify the flow rates
Let:
- Qin = flow rate of water entering the vessel = 100 cm³/s
- Aorifice = cross-sectional area of the hole = 1 cm²
- h = height of water in the vessel (in cm)
- g = acceleration due to gravity = 10 m/s² = 1000 cm/s² (since we need to convert to CGS units)
Step 3: Calculate the velocity of water exiting the hole
Using Torricelli's theorem, the velocity v of water exiting the hole can be given by:
v=√2gh
Substituting g in CGS units:
v=√2×1000×h=√2000h
Step 4: Calculate the flow rate of water exiting the hole
The flow rate Qout through the hole can be expressed as:
Qout=Aorifice⋅v
Substituting the values:
Qout=1⋅√2000h=√2000h
Step 5: Set up the equation for steady state
At steady state, the flow rate entering the vessel equals the flow rate exiting the vessel:
Qin=Qout
Substituting the known values:
100=√2000h
Step 6: Square both sides to eliminate the square root
1002=2000h
10000=2000h
Step 7: Solve for h
h=100002000=5 cm
Conclusion
The height of water in the vessel under steady state is 5 cm.
---
We have a cylindrical vessel that is 20 cm high and 10 cm in diameter. There is a hole at the bottom with a cross-sectional area of 1 cm², and water is entering the vessel at a rate of 100 cm³/s. We need to find the steady-state height of the water in the vessel.
Let:
- Qin = flow rate of water entering the vessel = 100 cm³/s
- Aorifice = cross-sectional area of the hole = 1 cm²
- h = height of water in the vessel (in cm)
- g = acceleration due to gravity = 10 m/s² = 1000 cm/s² (since we need to convert to CGS units)
Using Torricelli's theorem, the velocity v of water exiting the hole can be given by:
v=√2gh
Substituting g in CGS units:
v=√2×1000×h=√2000h
The flow rate Qout through the hole can be expressed as:
Qout=Aorifice⋅v
Substituting the values:
Qout=1⋅√2000h=√2000h
At steady state, the flow rate entering the vessel equals the flow rate exiting the vessel:
Qin=Qout
Substituting the known values:
100=√2000h
1002=2000h
10000=2000h
h=100002000=5 cm
The height of water in the vessel under steady state is 5 cm.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion and Reason
1 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cylindrical vessel open at the top has diameter 20cm and height 14cm. Find the cost of tin-plating it on the inside at the rate of 50 paise per hundred square centimetre.
View SolutionA chemical reaction takes place in a vessel of cross-sectional area 150 cm2. Due to the reaction , the piston of the vessel is moved upward by 15 cm against the external pressure of one atm. The work done by the system is
View SolutionA tube 1cm2 in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 ms−2 .

View SolutionA tube 1cm2 in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 ms−2 .

View SolutionThe level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View SolutionA large cylindrical vessel contains water to a height of 10 m. If is found that the thrust acting on the curved surface is equal to that at the bottom. If atmospheric pressure can support a water column of 10 m. the radius of the vessel is
View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
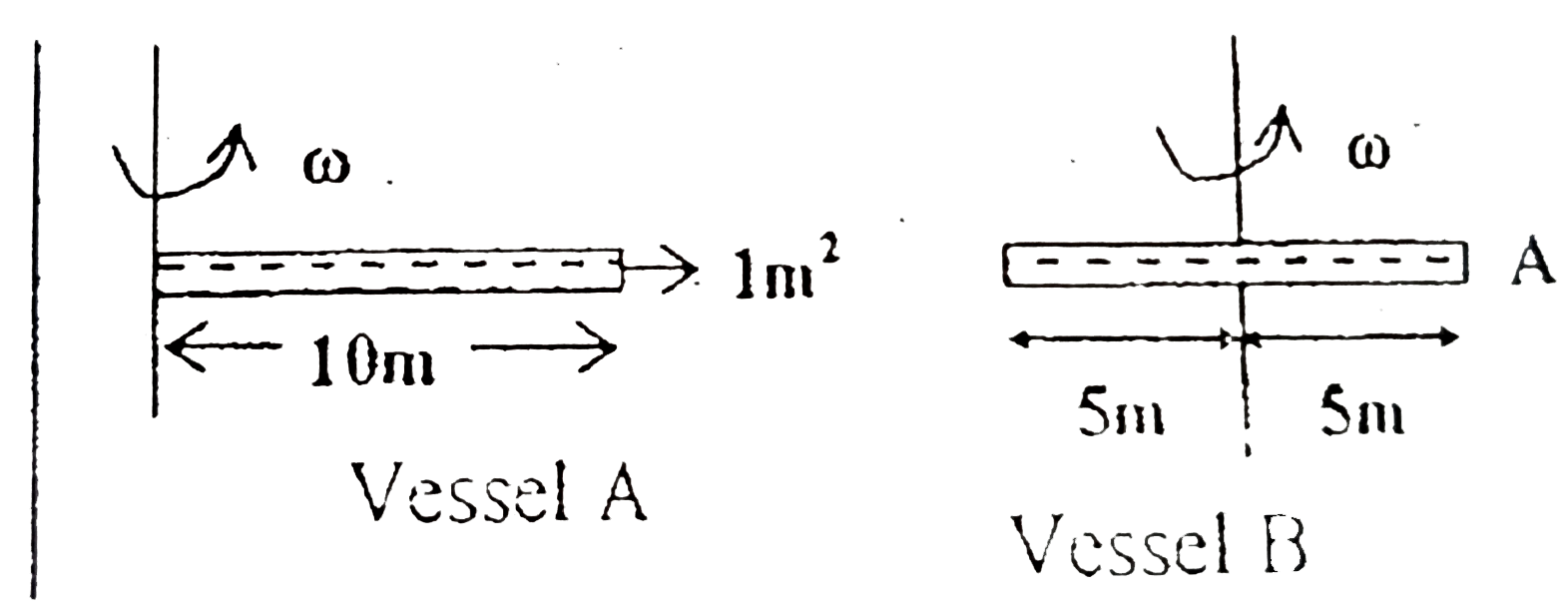
View SolutionA water hose pipe of cross-sectional area 5cm2 is used to fill a tank of 120L. It has been observed that it takes 2 min to fill the tank. Now, a nozzel with an opening of cross-sectional area 1cm2 is attached to the hose. The nozzel is held so that water is projected horizontally from a point 1m above the ground. The horizontal distance over which the water can be projected is (Take g=10m/s2).
View SolutionThe level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View Solution
