A thin wire is bent in the form of a ring of diameter 3.0cm.The ring is placed horizontally on the surface of soap solution and then raised up slowly. Upward force necessary to break the vertical film formed between the ring and the solution is
6πTdyne
2πTdyne
4πTdyne
3πTdyne
The correct Answer is:A
To solve the problem of finding the upward force necessary to break the vertical film formed between the ring and the soap solution, we can follow these steps:
Step 1: Understand the Problem
We have a thin wire bent into a ring with a diameter of 3.0 cm, which is placed on the surface of a soap solution. When we raise the ring, we need to calculate the upward force required to break the surface tension film that forms around the ring.
Step 2: Identify the Relevant Concepts
The upward force required to break the film is related to the surface tension of the liquid. Surface tension (T) acts along the perimeter of the ring, and since the film has two surfaces (inside and outside), we will consider both.
Step 3: Calculate the Circumference of the Ring
The circumference (C) of the ring can be calculated using the formula:
C=πd
where d is the diameter of the ring. Given that the diameter is 3.0 cm:
C=π×3.0 cm=3π cm
Step 4: Determine the Total Length of the Film
Since there are two surfaces of the film acting on the ring, the effective length (L) that contributes to the surface tension force is:
L=2×C=2×(3π)=6π cm
Step 5: Calculate the Upward Force
The upward force (F) necessary to break the film can be calculated using the formula:
F=T×L
Substituting the value of L:
F=T×(6π)
Step 6: Finalize the Expression for the Upward Force
Thus, the upward force required to break the vertical film is:
F=6πT dynes
Step 7: Conclusion
The upward force necessary to break the vertical film formed between the ring and the soap solution is 6πT dynes.
We have a thin wire bent into a ring with a diameter of 3.0 cm, which is placed on the surface of a soap solution. When we raise the ring, we need to calculate the upward force required to break the surface tension film that forms around the ring.
The upward force required to break the film is related to the surface tension of the liquid. Surface tension (T) acts along the perimeter of the ring, and since the film has two surfaces (inside and outside), we will consider both.
The circumference (C) of the ring can be calculated using the formula:
C=πd
where d is the diameter of the ring. Given that the diameter is 3.0 cm:
C=π×3.0 cm=3π cm
Since there are two surfaces of the film acting on the ring, the effective length (L) that contributes to the surface tension force is:
L=2×C=2×(3π)=6π cm
The upward force (F) necessary to break the film can be calculated using the formula:
F=T×L
Substituting the value of L:
F=T×(6π)
Thus, the upward force required to break the vertical film is:
F=6πT dynes
The upward force necessary to break the vertical film formed between the ring and the soap solution is 6πT dynes.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion and Reason
1 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A wire of some length is bent in the form of a ring of diameter 2a having self inductance L, then L will depend upon a as:
View SolutionA uniformly conducting wire is bent to form a ring of mass 'm' and radius 'r', and the ring is placed on a rough horizontal surface with its plane horizontal. There exists a uniform and constant horizontal magnetic field of induction B. Now a charge q is passed through the ring in a very small time interval Δt. As a result the ring ultimately just becomes vertical. Calculate the value of g(acceleration due to gravity) in terms of other given quantities. Assume that friction is sufficient to prevent slipping and ignore any loss in energy.
View Solution
Knowledge Check
A current I=10A flows in a ring of radius r0=15cm made of a very thin wire. The tensile strength of the wire is equal to T=1.5N. The ring is placed in a magnetic field, which is perpendicular to the plane of th ering so that the forces tend to break the ring. Find B ( in T) at which the ring is broken.
A0.5 TB1 TC2 TD2.5 T
A massless inextensible string in the form of a loop is placed on a horizontal film of soap solution of surface tension T. If film is pierced inside the loop and it convert into a circular loop of diameter d, then the tension produced in string is
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.

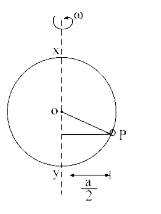
View SolutionA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then ω2 is equal to:
View SolutionTwo spherical soap bubbles of diameters 10 cm and 6 cm are formed, one at each end of a narrow horizontal glass tube. If the surface tension of the soap solution is 0.03Nm−1, then the pressure difference in pascal between the two ends of the tube is
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionThe vapour pressure of a solvent in a solution is lower than that of pure solvent, at the same temperature. A higher temperature is needed to raise the vapour pressure up to the atmospheric pressure, when boiling begins. However, increase is small, like 0.1molkg−1 aqueous sucrose solution boils at 100.05∘C.
Sea water, an aqueous solution, which is rich in Na+ and Cl− ions, freezes about 1∘C lower than frozen water. At the freezing point of a pure solvent, the rates at which two molecules stick together to form the solid and leave it to return to liquid state are equal when solute is present. Fewer solvent molecules are in contact with surface of solid. However, the rate at which the solvent molecules leave the surface of solid remains unchanged. That is why temperature is lowered to restore the equilibrium. The freezing point depression in an ideal solution is proportional to molality of the solute.
An aqueous solution of 0.1molkg−1 concentration of sucrose should have freezing point of (Kf=1.86)
View SolutionA constant horizontal force of 5N in magnitude is applied tangentially to the top most of a ring of mass 10 kg and radius 10 cm kept on a rough horizontal surface with coefficient of friction between surface and ring being 0.2. The friction force on the ring would be: (g=10m/s2)
View Solution
