Question

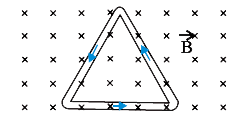
A wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.

Explanation

To solve the problem of finding the forces on the three sides of an equilateral triangle formed by a wire carrying current in a magnetic field, we can follow these steps:

Step 1: Understand the Given Data
- The wire is bent into an equilateral triangle PQR with each side measuring 10 cm.
- The current (I) flowing through the wire is 5.0 A.
- The magnetic field (B) has a magnitude of 2.0 T and is directed perpendicularly to the plane of the triangle.

Step 2: Convert Units
Convert the side length from centimeters to meters:
- \( L = 10 \, \text{cm} = 10 \times 10^{-2} \, \text{m} = 0.1 \, \text{m} \)

Step 3: Calculate the Force on One Side
The force on a straight current-carrying conductor in a magnetic field is given by the formula:
\( F = I \cdot L \cdot B \cdot \sin(\theta) \)
Where:
- \( I \) = current (5.0 A)
- \( L \) = length of the side (0.1 m)
- \( B \) = magnetic field (2.0 T)
- \( \theta \) = angle between the current direction and the magnetic field direction (90° since the magnetic field is perpendicular)

Since \( \sin(90°) = 1 \), the formula simplifies to:
\( F = I \cdot L \cdot B \)

Substituting the values:
\( F = 5.0 \, \text{A} \cdot 0.1 \, \text{m} \cdot 2.0 \, \text{T} \)
\( F = 1.0 \, \text{N} \)

Step 4: Determine the Force on All Three Sides
Since the triangle is equilateral and the current is the same in all sides, the force on each side (PQ, QR, RP) will be the same:
- \( F_{PQ} = F_{QR} = F_{RP} = 1.0 \, \text{N} \)

Step 5: Determine the Direction of the Forces
Using the right-hand rule:
- For side PQ, if the thumb points in the direction of the current and the fingers point in the direction of the magnetic field, the palm will face the direction of the force.
- For side QR, the force will be directed in a different direction, and similarly for side RP.

Step 6: Analyze the Net Force
Since the triangle is symmetrical:
- The forces on sides QR and RP will have components that cancel each other out in the horizontal direction.
- The vertical components will also cancel out, leading to a net force of zero.

Conclusion
The forces on each side of the triangle are:
- \( F_{PQ} = 1.0 \, \text{N} \)
- \( F_{QR} = 1.0 \, \text{N} \)
- \( F_{RP} = 1.0 \, \text{N} \)

The net force acting on the triangle is zero due to the symmetry of the forces.

---