A body is attached to a spring whose other end is fixed. If the spring is elongated by x, its potential energy is U=5x2, where x is in metre and U is in joule. U-x graph is




The correct Answer is:A
To solve the problem of finding the U-x graph for the given potential energy equation U=5x2, we can follow these steps:
Step 1: Understand the Given Equation
The potential energy U is given by the equation:
U=5x2
where U is in joules and x is in meters.
Step 2: Identify the Nature of the Equation
The equation U=5x2 is a quadratic equation in terms of x. Since it is in the form U=ax2 (where a=5), we can conclude that the graph will be a parabola.
Step 3: Determine the Orientation of the Parabola
Since the coefficient of x2 (which is 5) is positive, the parabola opens upwards. This means that as x increases or decreases from zero, the potential energy U will increase.
Step 4: Find the Value of Potential Energy at x=0
To find the y-intercept of the graph, we can substitute x=0 into the equation:
U=5(0)2=0
This indicates that when x=0, U=0. Therefore, the graph will pass through the origin (0,0).
Step 5: Sketch the Graph
Based on the above information, we can sketch the graph:
- The graph is a parabola that opens upwards.
- It passes through the origin (0,0).
Step 6: Analyze the Options
If presented with multiple-choice options, we would look for a graph that:
- Is a parabola opening upwards.
- Passes through the origin (0,0).
Conclusion
Based on the analysis, the correct U-x graph is the one that is a parabola opening upwards and passes through the origin.
---
The potential energy U is given by the equation:
U=5x2
where U is in joules and x is in meters.
The equation U=5x2 is a quadratic equation in terms of x. Since it is in the form U=ax2 (where a=5), we can conclude that the graph will be a parabola.
Since the coefficient of x2 (which is 5) is positive, the parabola opens upwards. This means that as x increases or decreases from zero, the potential energy U will increase.
To find the y-intercept of the graph, we can substitute x=0 into the equation:
U=5(0)2=0
This indicates that when x=0, U=0. Therefore, the graph will pass through the origin (0,0).
Based on the above information, we can sketch the graph:
- The graph is a parabola that opens upwards.
- It passes through the origin (0,0).
If presented with multiple-choice options, we would look for a graph that:
- Is a parabola opening upwards.
- Passes through the origin (0,0).
Based on the analysis, the correct U-x graph is the one that is a parabola opening upwards and passes through the origin.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
The potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View SolutionA single conservative fore Fx acts on a 2kg particle that moves along the x-axis. The potential energy is given by.
U=(x−4)2−16
Here, x is in metre and U in joule. At x=6.0m kinetic energy of particle is 8J find .
(a) total mechanical energy
(b) maximum kinetic energy
(c) values of x between which particle moves
(d) the equation of Fx as a funcation is zero
(e) the value of x at which Fx is zero .
View Solution
Knowledge Check
A long spring is stretched by 2 cm, its potential energy is U. IF the spring is stretched by 10 cm, the potential energy stored in it will be
AU/25BU/5C5 UD25 U
Let gravitational potential energy U is given by U=A√xB+x2, where x is distance. The dimensional formula of A/B is
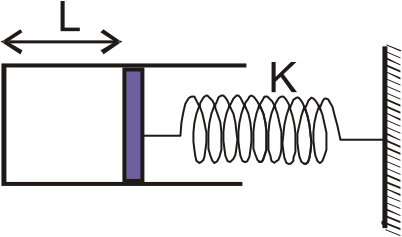
View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
View SolutionA body of mass M is attached to lower end of a metal wire whose upper End is fixed. The elongation is l. The ratio of loss of gravitational potential energy to the energy stored in the wire is
View SolutionA long elastic spring is stretched by 2cm and its potential energy is U. If the spring is stretched by 10cm, the PE will be
View SolutionA partical of mass 2kg is moving on the x−axis with a constant mechanical energy 20J. Its potential energy at any x is U=(16−x2)J where x is in metre. The minimum velocity of particle is :−
View SolutionAssuming that potential energy of spring is zero when it is stretched by x02, its potential energy when it is compressed by x0 is
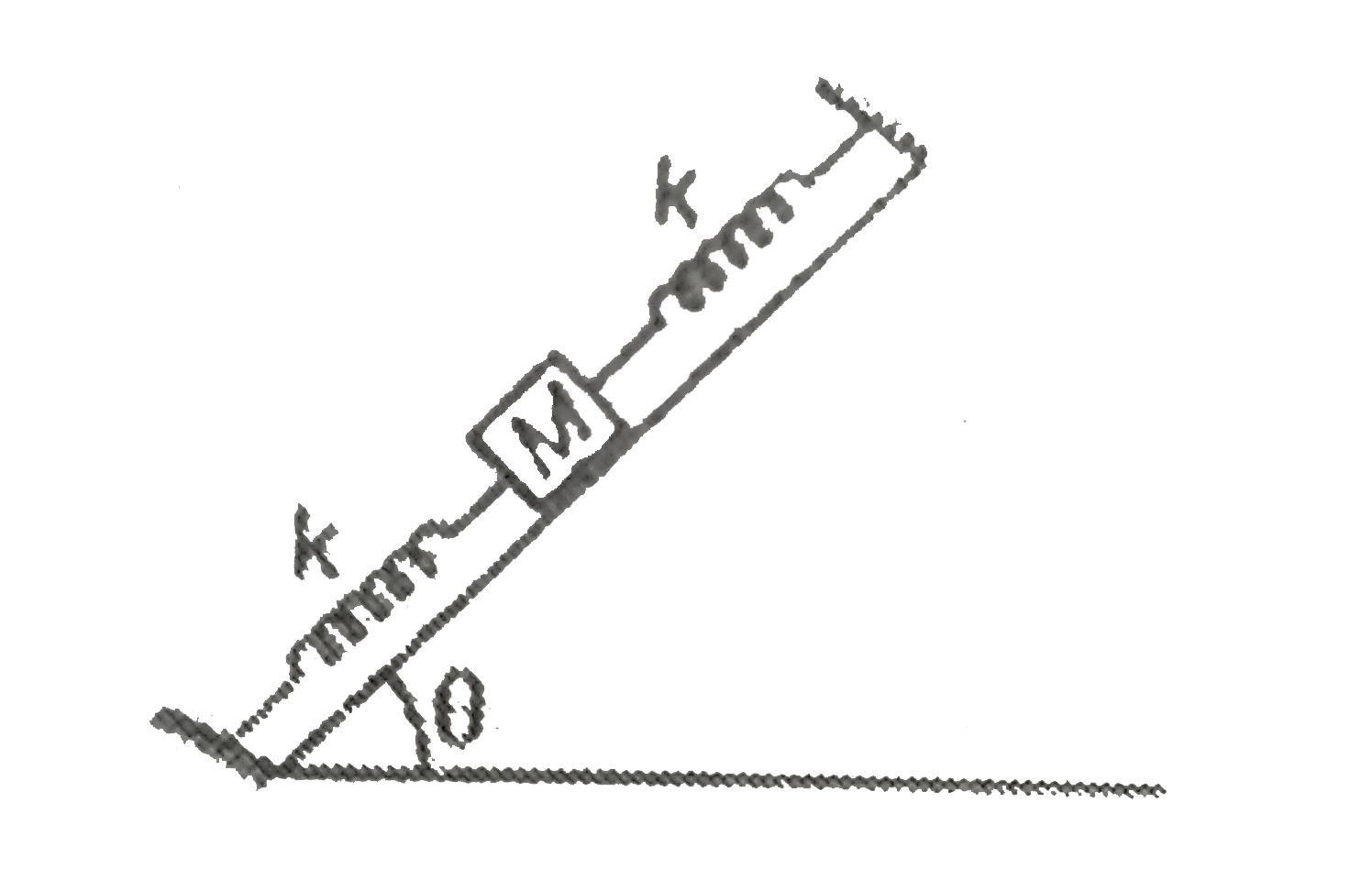
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View Solution
