A particle starts moving with constant, velocity v=2ms, from position x=5m The position time graph will be


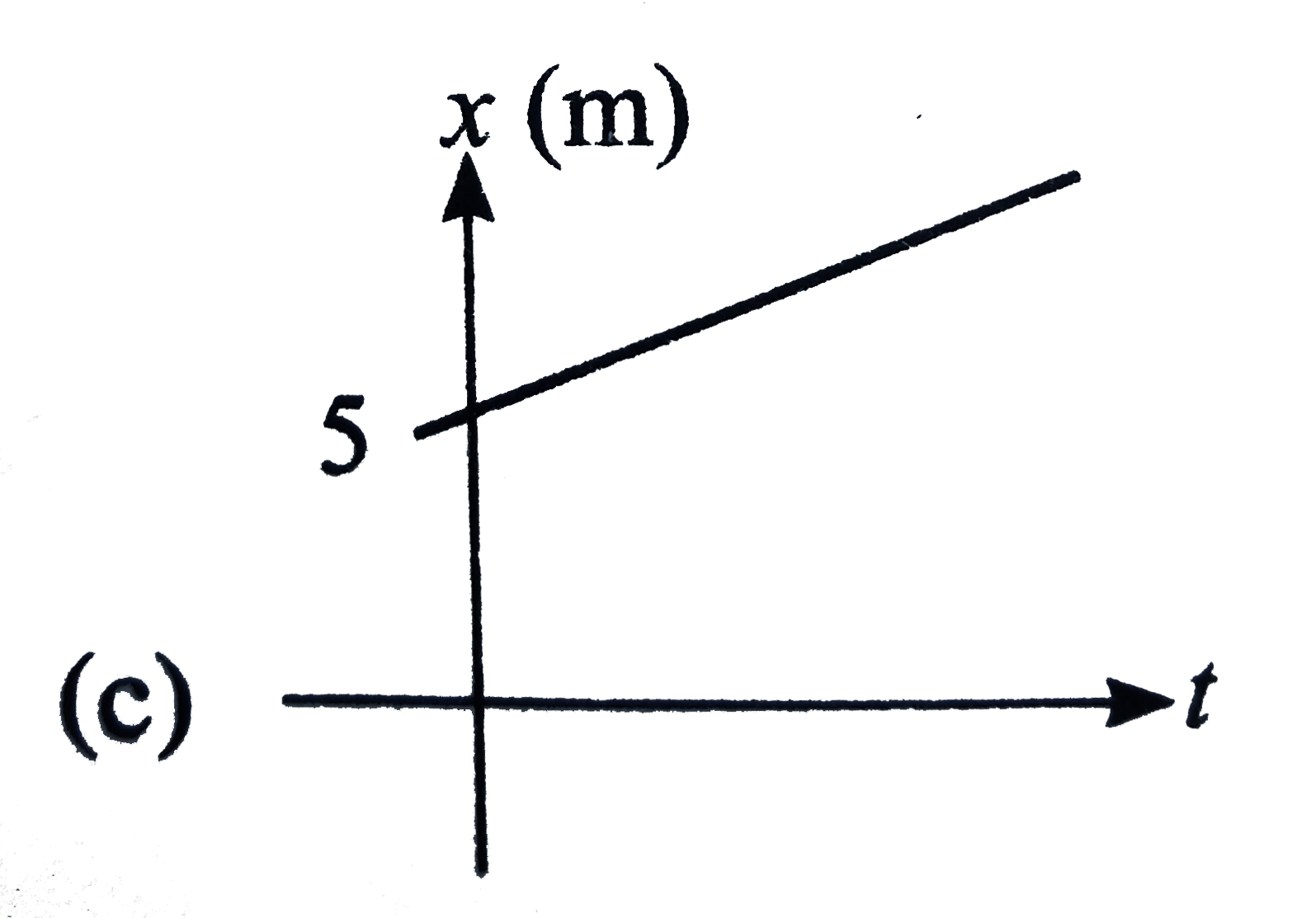
The correct Answer is:C
To solve the problem of finding the position-time graph for a particle moving with a constant velocity, we can follow these steps:
Step 1: Understand the given information
The particle starts at position x=5m and moves with a constant velocity v=2m/s.
Step 2: Set up the equation of motion
Since the particle is moving with constant velocity, we can use the equation of motion:
x(t)=x0+vt
where:
- x(t) is the position at time t,
- x0 is the initial position,
- v is the constant velocity,
- t is the time.
Step 3: Substitute the known values
Given that x0=5m and v=2m/s, we substitute these values into the equation:
x(t)=5+2t
Step 4: Analyze the equation
The equation x(t)=5+2t is a linear equation in the form y=mx+c, where:
- m (the slope) is 2,
- c (the y-intercept) is 5.
Step 5: Draw the graph
1. The y-intercept (where t=0) is at x=5m.
2. The slope of the line is 2, which means for every 1 second that passes, the position increases by 2m.
3. Thus, the graph will be a straight line starting from the point (0,5) and rising with a slope of 2.
Step 6: Identify the characteristics of the graph
- The graph is a straight line with a positive slope.
- The line crosses the y-axis at 5m.
Conclusion
The position-time graph of the particle is a straight line starting at (0,5) and rising with a slope of 2.
The particle starts at position x=5m and moves with a constant velocity v=2m/s.
Since the particle is moving with constant velocity, we can use the equation of motion:
x(t)=x0+vt
where:
- x(t) is the position at time t,
- x0 is the initial position,
- v is the constant velocity,
- t is the time.
Given that x0=5m and v=2m/s, we substitute these values into the equation:
x(t)=5+2t
The equation x(t)=5+2t is a linear equation in the form y=mx+c, where:
- m (the slope) is 2,
- c (the y-intercept) is 5.
1. The y-intercept (where t=0) is at x=5m.
2. The slope of the line is 2, which means for every 1 second that passes, the position increases by 2m.
3. Thus, the graph will be a straight line starting from the point (0,5) and rising with a slope of 2.
- The graph is a straight line with a positive slope.
- The line crosses the y-axis at 5m.
The position-time graph of the particle is a straight line starting at (0,5) and rising with a slope of 2.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Multiple correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
A particle starts moving with initial velocity 3m/s along x- axis from origin. Its acceleration is varying with x co-ordinate in parobalic nature as shown in the figure. At x=1m, tangent to the graph makes an angle 45∘ with positive x- aixs. Then at x=3m,

View SolutionAt t=0, a particle at (1,0,0) moves towards point (4,4,12) with a constant velocity of magnitude 65m/s. The position of the particle is measured in metres and time in sec. Assuming constant velocity, the position of the particle at t=2sec is :
View SolutionA car breaks a traffic signal with a speed of 40m/s. After 2s, a policeman starts following him with a constant acceleration of 12.5m/s2. Taking the position of signal to be origin, correct position time graph would be
View SolutionA body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

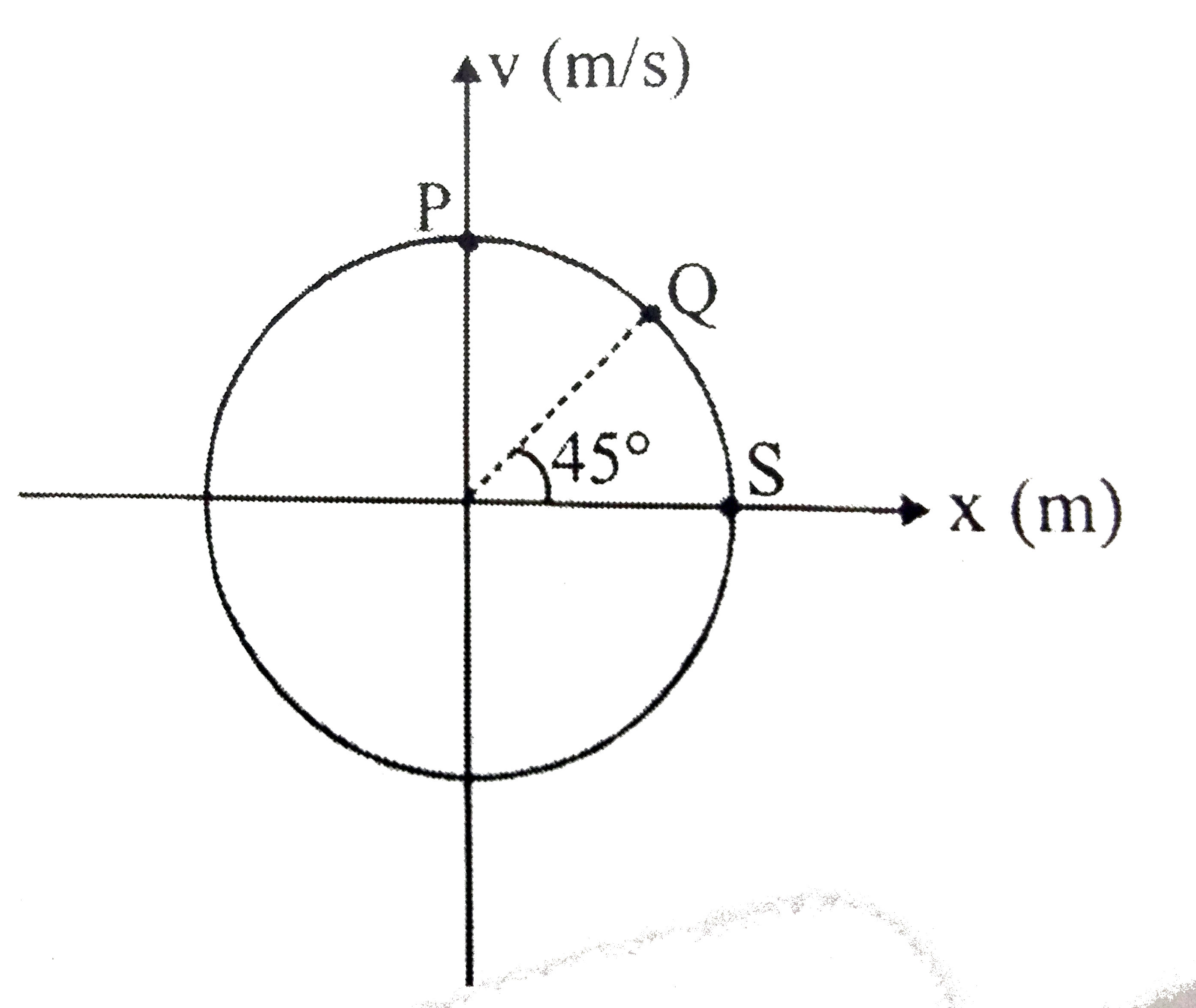
View SolutionA particle is in motion on the x-axis. The variation ofits velocity with position is as shown. The graph is circle and its equation is x2+v2=1, where x is in m and v in m/s. The correct statement(s) is/are:-
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?
View SolutionTwo particles A and B are initially 40mapart, A is behind B. Particle A is moving with uniform velocity of 10ms−1 towared B. Particle B starts moving away from A with constant acceleration of 2ms−1.
The time which there is a minimum distance between the two is .
View SolutionA particle starts from origin O from rest and moves with a uniform acceleration along the positive x=axis. Identify all figures that correctly represent the motion qualitatively. (a=acceleration , v=velocity,
x=displacement,t=time)

View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View Solution