The area of a rectangle will be maximum for the given perimeter, when rectangle is a
parallelogram
trapezium
square
none of these
The correct Answer is:C
To solve the problem of maximizing the area of a rectangle given a fixed perimeter, we can follow these steps:
1. Define the Perimeter: Let the perimeter of the rectangle be P. For a rectangle with sides A and B, the perimeter is given by:
P=2A+2B
Therefore, we can express the relationship as:
A+B=P2
2. Express One Variable in Terms of the Other: From the equation A+B=P2, we can express B in terms of A:
B=P2−A
3. Write the Area Function: The area A of the rectangle is given by:
Area=A×B
Substituting for B:
Area=A(P2−A)=P2A−A2
4. Differentiate the Area Function: To find the maximum area, we differentiate the area function with respect to A:
d(Area)dA=P2−2A
5. Set the Derivative to Zero: To find the critical points, set the derivative equal to zero:
P2−2A=0
Solving for A:
2A=P2⟹A=P4
6. Find the Corresponding Value of B: Substitute A=P4 back into the equation for B:
B=P2−A=P2−P4=P4
7. Conclusion: Since both sides A and B are equal, we conclude that the rectangle is a square. Therefore, the area of the rectangle is maximized when the rectangle is a square.
Final Answer:
The area of a rectangle will be maximum for the given perimeter when the rectangle is a square.
---
P=2A+2B
Therefore, we can express the relationship as:
A+B=P2
B=P2−A
Area=A×B
Substituting for B:
Area=A(P2−A)=P2A−A2
d(Area)dA=P2−2A
P2−2A=0
Solving for A:
2A=P2⟹A=P4
B=P2−A=P2−P4=P4
The area of a rectangle will be maximum for the given perimeter when the rectangle is a square.
Similar Questions
Knowledge Check
A rectangle is 5 times as wide as it is long. The area of the rectangle is 320 square feet. What is the perimeter of the rectangle , in feet ?
A8B40C48D96The length of rectangle is double the breadth , If the minimum perimeter of the rectangle is 120 cm , then
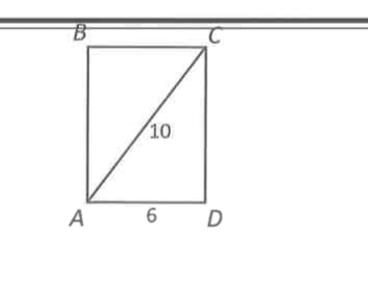
Abreadth >20 cmBbreadth <20 cmCbreadth ≥20 cmDbreadth ≤20 cmAC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
A7B14C17D20
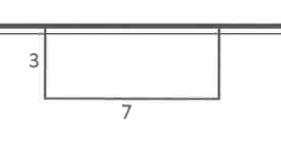
Find the perimeter of each rectangle.
View SolutionThe perimeter of a rectangle is 40 cm. Find the dimensions of the rectangle if its area is maximum.
View SolutionA square and a rectangle have equal area. If side of a square is 24 cm and the length of the rectangle is 32 cm , find
the perimeter of the rectangle.
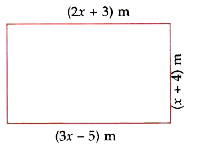
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
View SolutionThe perimeter of a rectangle is 30 cm. If the lengths of the sides of the rectangles are natural numbers, find all rectangles with same perimeter and also find their respective areas.
View Solution