AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
7
14
17
20
The correct Answer is:B
To solve the problem step by step, we need to find the perimeter of rectangle ABCD given that the diagonal AC measures 5 units and the area of the rectangle is 12 square units.
Step 1: Define Variables
Let the length of the rectangle be L and the breadth be B.
Step 2: Use Area Formula
The area A of a rectangle is given by the formula:
A=L×B
Given that the area is 12 square units, we can write:
L×B=12(1)
Step 3: Use Diagonal Formula
The diagonal d of a rectangle can be calculated using the Pythagorean theorem:
d2=L2+B2
Given that the diagonal AC measures 5 units, we have:
52=L2+B2
This simplifies to:
25=L2+B2(2)
Step 4: Substitute for B
From equation (1), we can express B in terms of L:
B=12L
Now substitute B into equation (2):
25=L2+(12L)2
This expands to:
25=L2+144L2
Step 5: Multiply Through by L2
To eliminate the fraction, multiply the entire equation by L2:
25L2=L4+144
Rearranging gives us:
L4−25L2+144=0(3)
Step 6: Let M=L2
Let M=L2. Then equation (3) becomes:
M2−25M+144=0
Step 7: Solve the Quadratic Equation
Now we will solve this quadratic equation using the quadratic formula:
M=−b±√b2−4ac2a
Here, a=1,b=−25,c=144:
M=25±√(−25)2−4⋅1⋅1442⋅1
Calculating the discriminant:
M=25±√625−5762
M=25±√492
M=25±72
This gives us two possible values for M:
M=322=16orM=182=9
Step 8: Find Length and Breadth
Since M=L2, we have:
1. If M=16, then L=4 (since length cannot be negative).
2. If M=9, then L=3.
Now we can find B:
- For L=4:
B=124=3
- For L=3:
B=123=4
Thus, the dimensions of the rectangle are L=4 and B=3 (or vice versa).
Step 9: Calculate Perimeter
The perimeter P of a rectangle is given by:
P=2(L+B)
Substituting the values:
P=2(4+3)=2×7=14 units
Final Answer
The perimeter of the rectangle is 14 units.
---
Let the length of the rectangle be L and the breadth be B.
The area A of a rectangle is given by the formula:
A=L×B
Given that the area is 12 square units, we can write:
L×B=12(1)
The diagonal d of a rectangle can be calculated using the Pythagorean theorem:
d2=L2+B2
Given that the diagonal AC measures 5 units, we have:
52=L2+B2
This simplifies to:
25=L2+B2(2)
From equation (1), we can express B in terms of L:
B=12L
Now substitute B into equation (2):
25=L2+(12L)2
This expands to:
25=L2+144L2
To eliminate the fraction, multiply the entire equation by L2:
25L2=L4+144
Rearranging gives us:
L4−25L2+144=0(3)
Let M=L2. Then equation (3) becomes:
M2−25M+144=0
Now we will solve this quadratic equation using the quadratic formula:
M=−b±√b2−4ac2a
Here, a=1,b=−25,c=144:
M=25±√(−25)2−4⋅1⋅1442⋅1
Calculating the discriminant:
M=25±√625−5762
M=25±√492
M=25±72
This gives us two possible values for M:
M=322=16orM=182=9
Since M=L2, we have:
1. If M=16, then L=4 (since length cannot be negative).
2. If M=9, then L=3.
- For L=4:
B=124=3
- For L=3:
B=123=4
The perimeter P of a rectangle is given by:
P=2(L+B)
Substituting the values:
P=2(4+3)=2×7=14 units
The perimeter of the rectangle is 14 units.
Similar Questions
Knowledge Check
A rectangle is 5 times as wide as it is long. The area of the rectangle is 320 square feet. What is the perimeter of the rectangle , in feet ?
A8B40C48D96In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
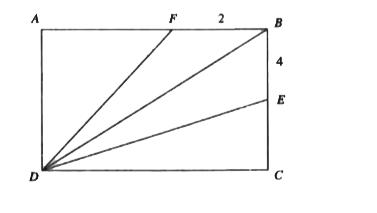 A18B23C30D42
A18B23C30D42
If the rectangle above has an area of 32, and the unshaded triangles are isosceles, what is the perimeter of the shaded area?A16B10+7√2C10+12√2D32
The area of a rectangle will be maximum for the given perimeter, when rectangle is a
View SolutionArea of a rectangle of breadth 17cm is 340cm2. Find the perimeter of the rectangle.
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
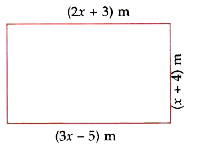
View SolutionThe length of a rectangle exceeds its width by 8 cm and the area of the rectangle is 240 sq. cm. Find the dimensions of the rectangle.
View SolutionIn the figure, the ratio of the area of parallelogram ABCD to the area of rectangle AECF is 5 : 3. What is the area of the rectangle AECF?
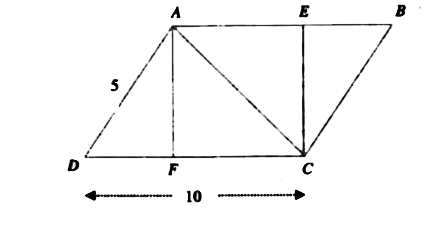
View Solution