Question

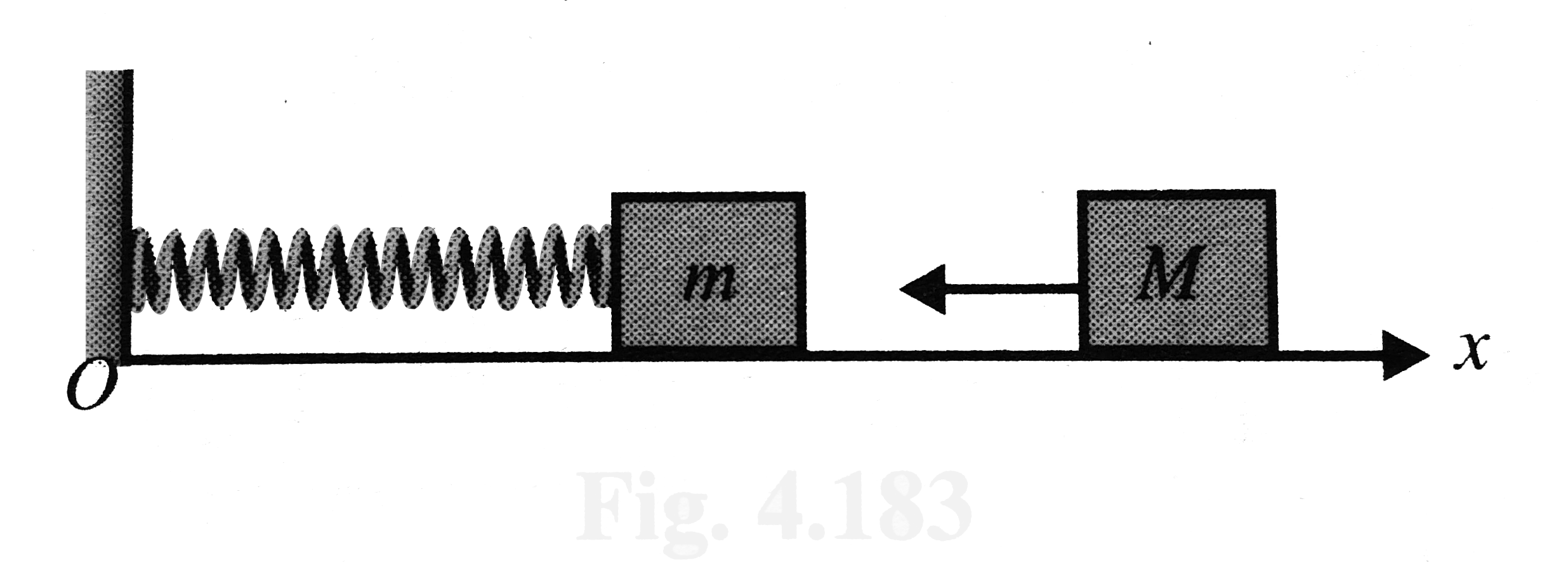
One end of an ideal spring in fixed in a wall at origin O and axis of spring is paralllel to the x-axis . A block of mass $m=1kg$ is attached to the free end of the spring and it is performing SHm. Equation of position of the block in coordinate system Shown in Fig. is $x=10+3\sin \left(10t\right)$, where t is in second and x in cm. Another block of mass $M=3kg$ moving towards the origin with velocity $30\frac{cm}{s}$ collides with the block performing SHM at $t=0$ and gets stuck to it.
Q. Angular frequency of oscillation after collision is

Options

A. 3 cm
B. 20 cm
C. 10 cm
D. 100 cm

Answer

A

Explanation

Conserving linear momentum
`(1+3)v=1xx0.3+3(-0.3)`
`v=-0.15(m)/(s)`
Negative sign indicates that combined body starts to move leftwards. But at the instant of collision, spring is in its natural length or combined by is in equilibrium position. Hence at `t=0`, phase of combinied body becomes equal to `pi`.
Therefore new amplitude of oscillaion is
`a'=(|a|)/(omega)=(0.15)/(5)=0.03m=3cm`