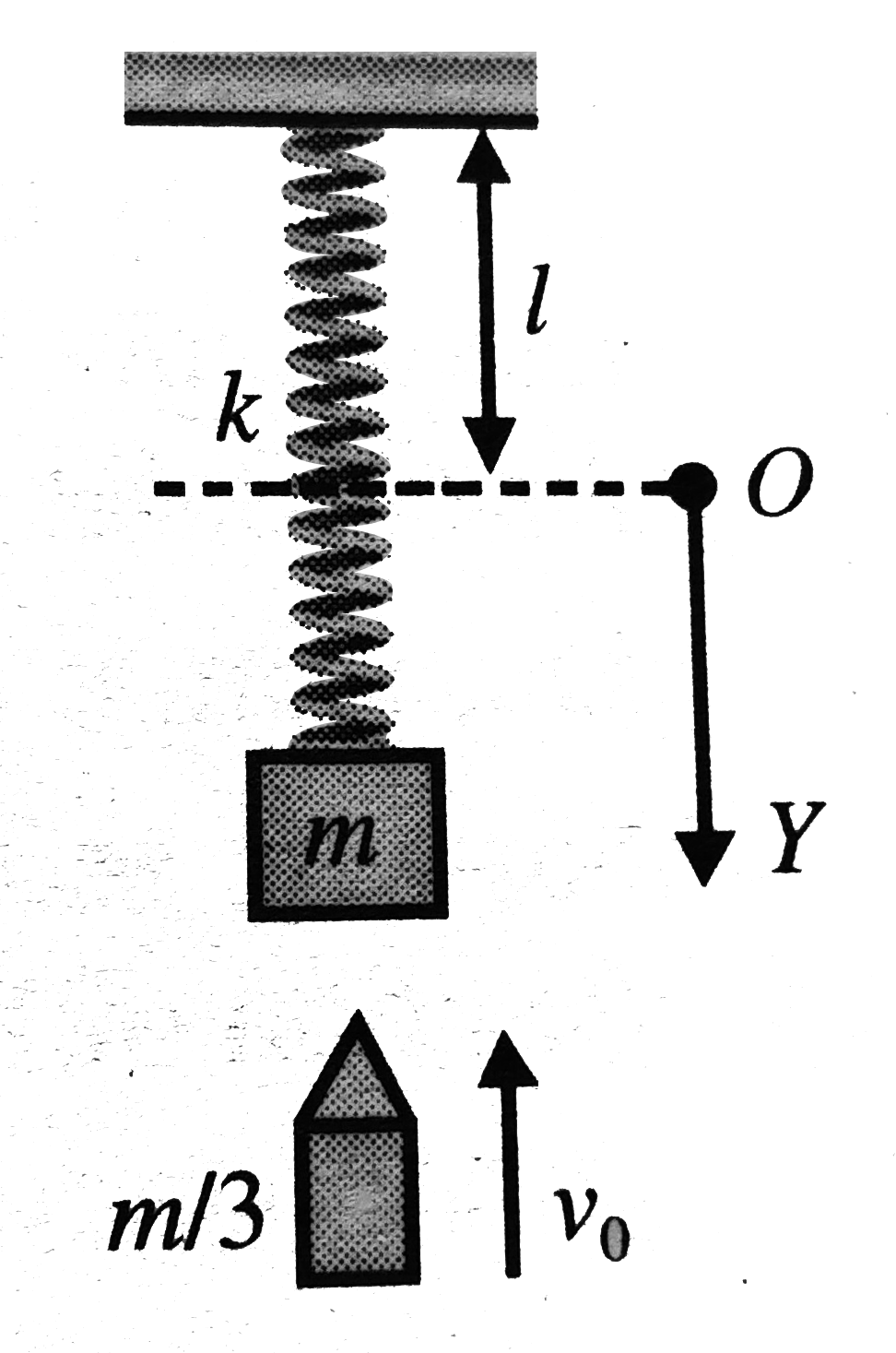
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
√4m3k[cos−1(mg3kA)−cos−1(4mg3kA)]
√3k4m[cos−1(mg3kA)−cos−1(4mg3kA)]
√4m6k[sin−1(4mg3kA)−sin−1(mg3kA)]
none of these
The correct Answer is:A
Initially in equilibrium let the elongation in spring be y0 then mg=ky0
y0=mgk As the bullet strikes the block with velocity with velocity v0 and gets embed ded into it, the velocity of the combined mass can be computed by ising the principle of moment conservation.
m3v0=4m3v⇒v=v04
Let new mean position is at distance y from the origin, then
ky=4m3g⇒y=4mg3k
Now, the block executes SHM about mean position defined by y=4mg3k with time period T=2π√4m3k. At t=0, the combined mass is at a displacement of (y−y0) from mean position and is moving with velocity v, then by using v=ω√A2−x2, we can find the amplitude of motion,
(v04)2=3k4m[A2−(y−y0)2]=3k4m[A2−(mg3k)2]
⇒A=√mv2012k+(mg3k)2
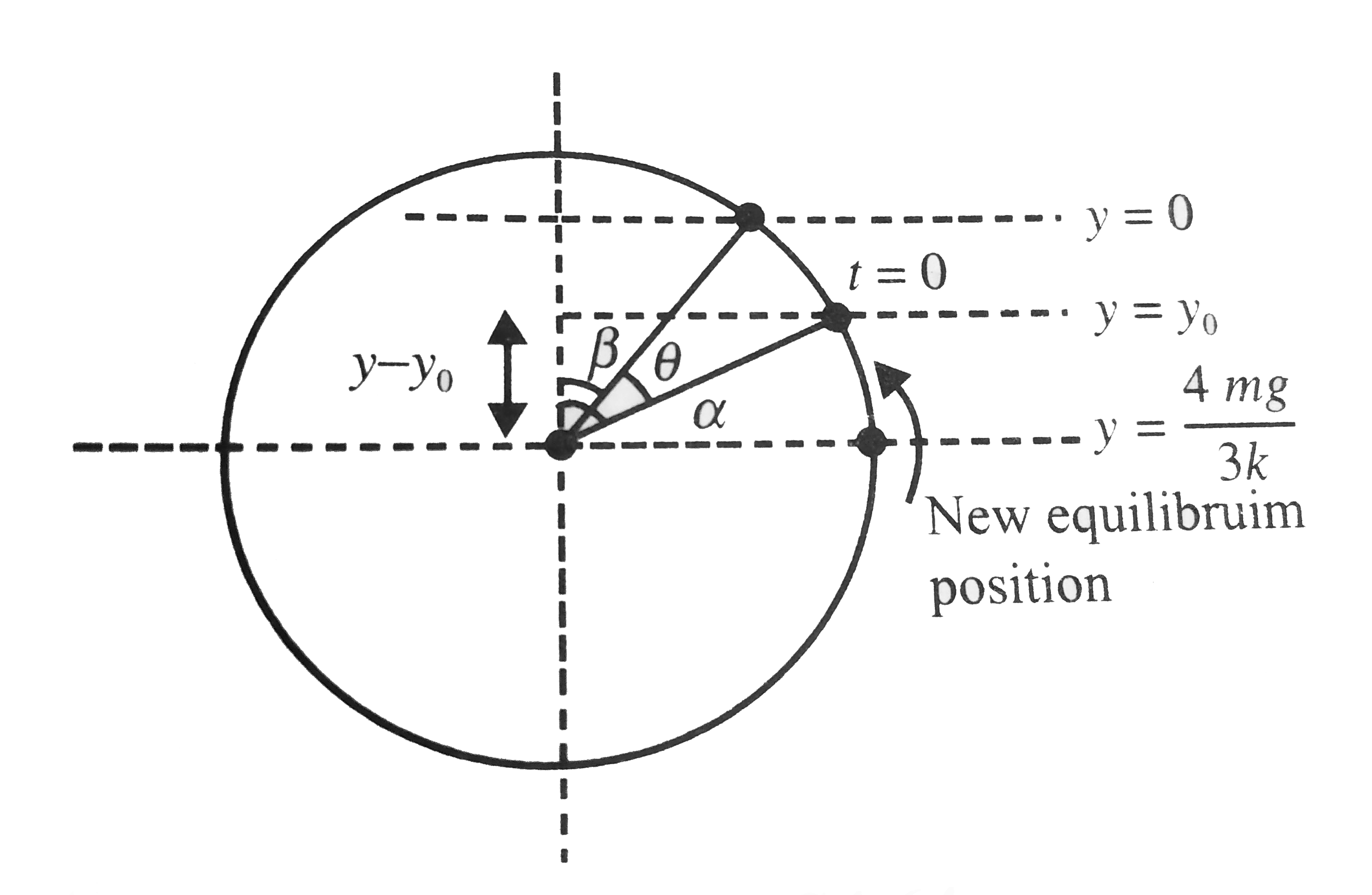
To compute the time taken by the combined mass from y=mgk to y=0, we can either go for equation method of circular motion projection method.
Required time, t=θω=α−βω
cosα=y−y0A=⎛⎜⎝4mg3k−4mgkA⎞⎟⎠=mg3kA
cosβ=yA=4mg3kA
So, t=cos−1(mg3kA)−cos−1(4mg3kA)ω
=√4m3k[cos−1(mg3kA)−cos−1(4mg3kA)]
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
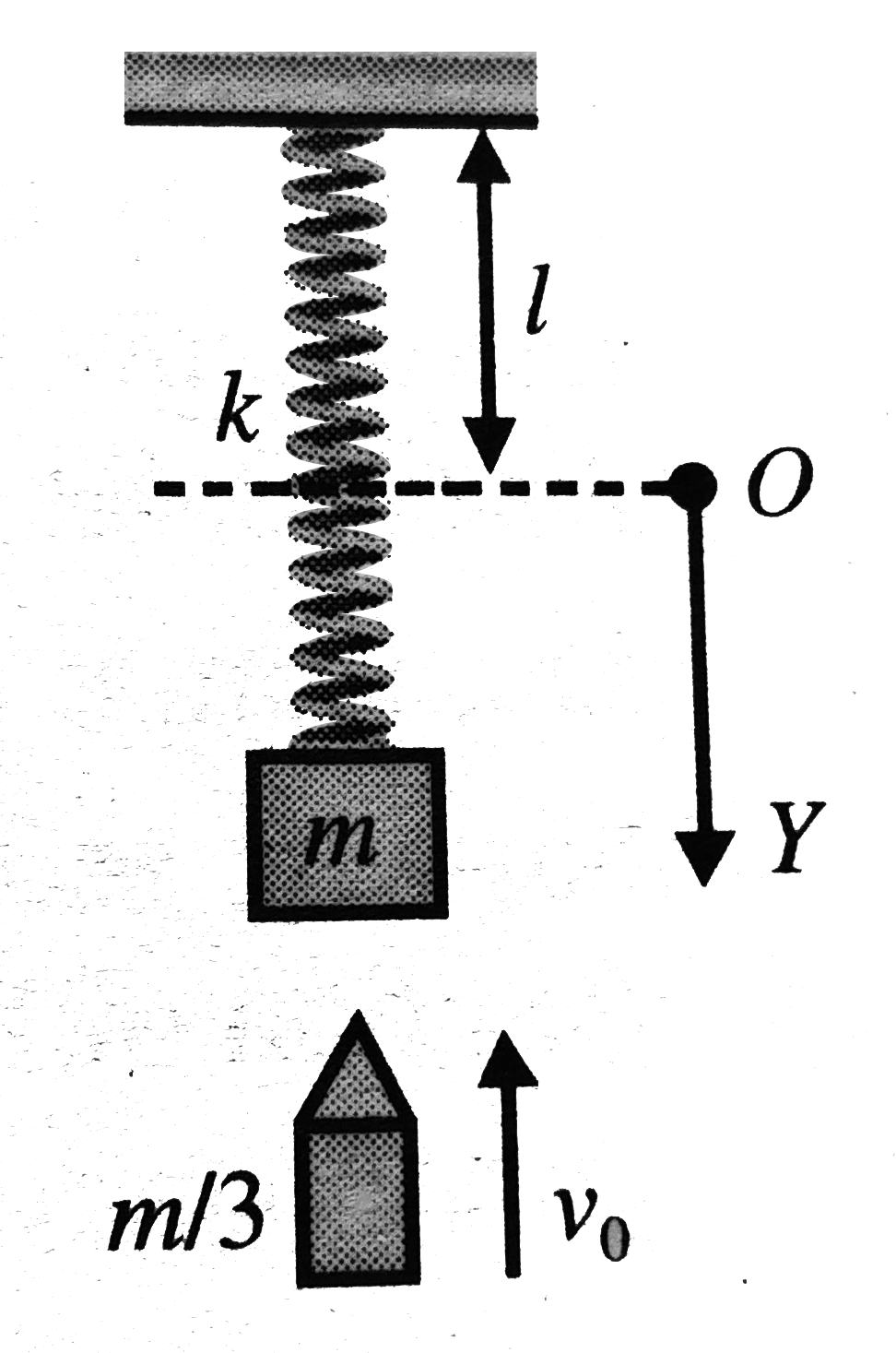
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The amplitude of oscillation would be
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
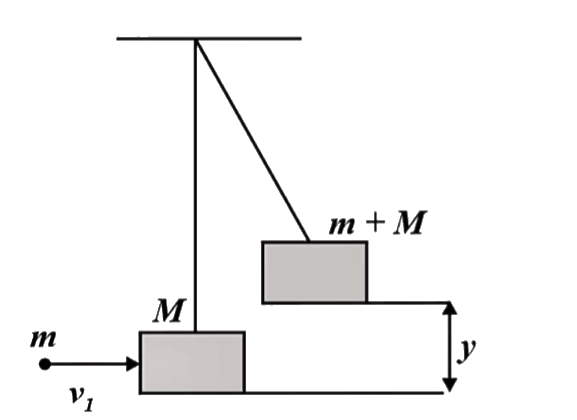
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
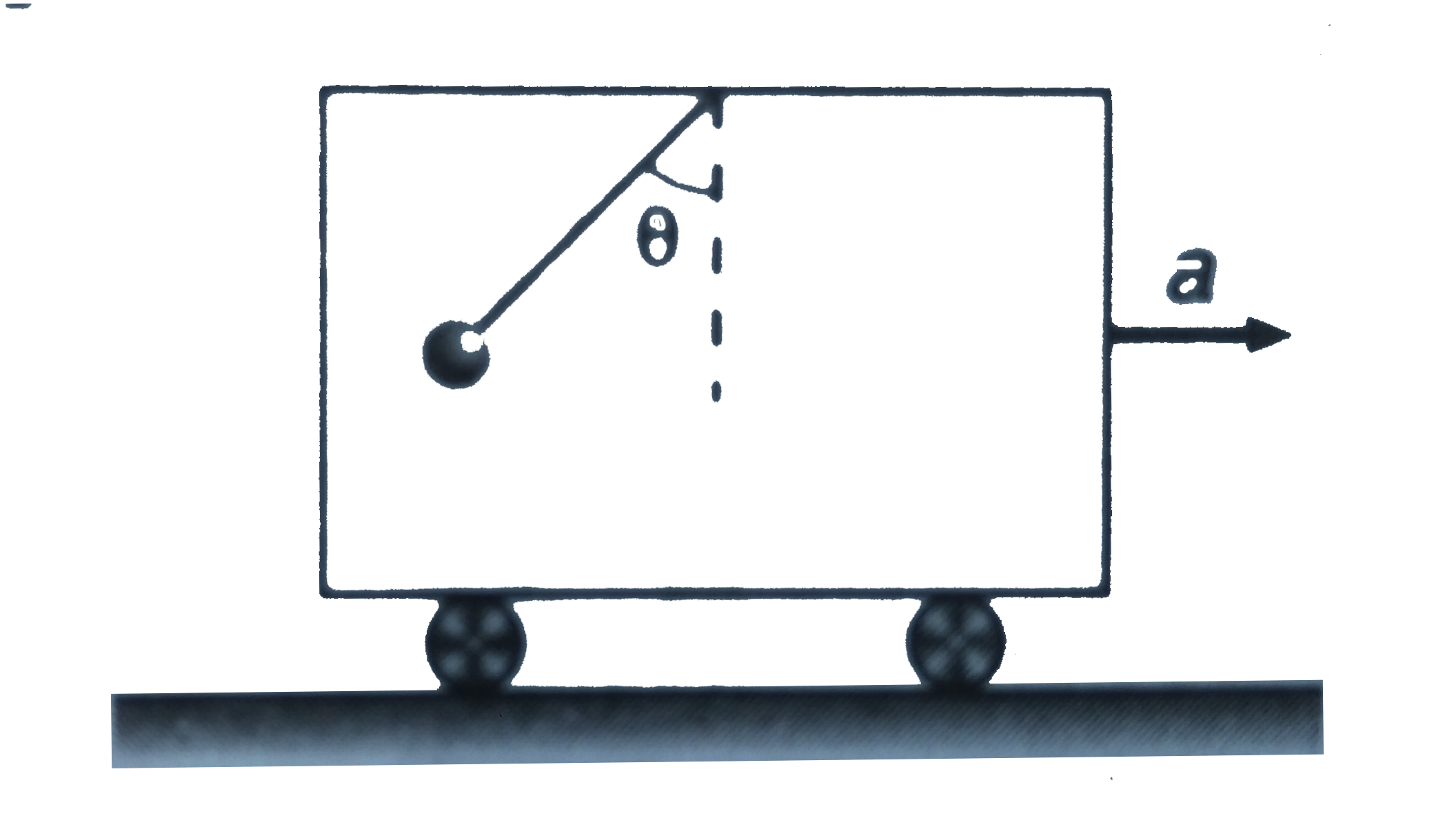
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
View SolutionA spring block pendulum is shown in figure . The system is hanging in equilibrium. A bullet of mass m/2 moving at a speed u bites the block from downwards direction and gets embedded in it. Find the amplitude of oscillation of the block now.

View SolutionA block of known mass is suspended from a fixed support through a ligh spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
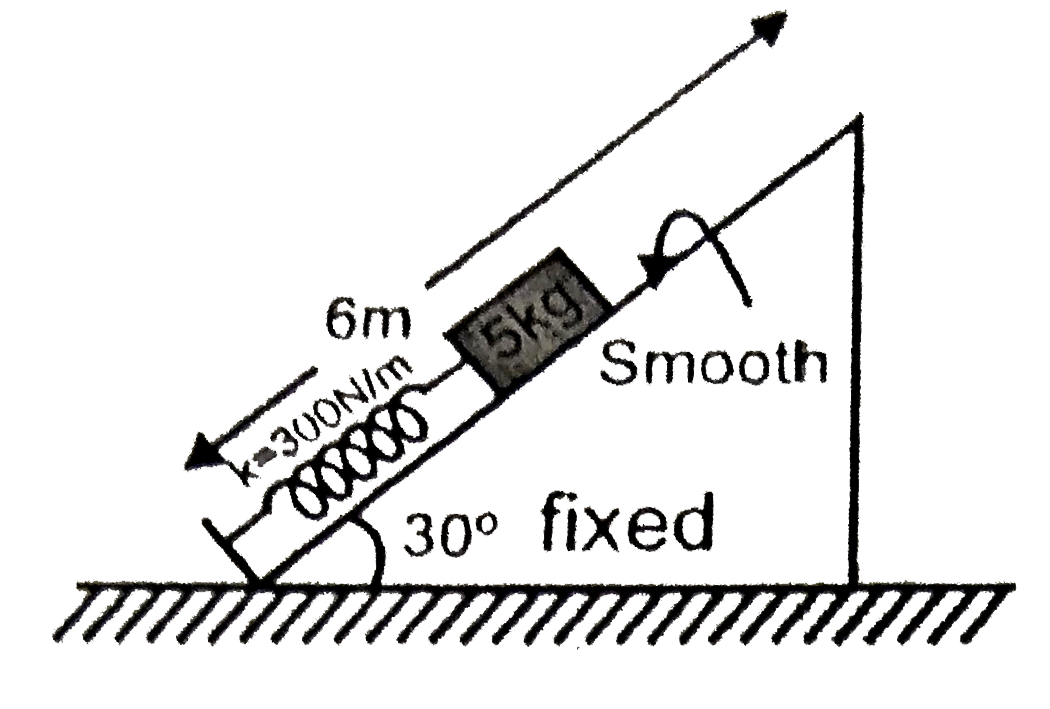
View SolutionA block of mass 5kg is released from rest when compression in spring is 2m. Block is not attached with spring and natural length of the spring in 4m. Maximum height of block from ground is :(g=10m/s2)
View Solution
