A plank with a small block on top of it is under going vertical SHM. Its period is 2sec. The minium amplitude at which the block will separate from plank is :
10π2
π210
20π2
20π2
The correct Answer is:A
To solve the problem, we need to determine the minimum amplitude at which a block will separate from a plank undergoing vertical simple harmonic motion (SHM). Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Condition for Separation
The block will separate from the plank when the normal force acting on it becomes zero. This occurs when the upward acceleration of the plank due to SHM exceeds the acceleration due to gravity (g).
Step 2: Relate Acceleration in SHM to Gravity
In SHM, the maximum acceleration (a_max) can be expressed as:
amax=ω2A
where:
- ω is the angular frequency,
- A is the amplitude of the motion.
For the block to separate, we need:
amax>g
This leads to:
ω2A>g
Step 3: Express Angular Frequency in Terms of Period
The angular frequency ω is related to the period T by the formula:
ω=2πT
Given that the period T is 2 seconds, we can calculate ω:
ω=2π2=πrad/s
Step 4: Substitute ω into the Acceleration Condition
Substituting ω into the inequality:
π2A>g
Thus, we can express the amplitude A as:
A>gπ2
Step 5: Calculate the Minimum Amplitude
Now, substituting g (approximately 10 m/s²):
A>10π2
Step 6: Calculate the Numerical Value
Calculating π2 (approximately 9.87):
A>109.87≈1.01m
Conclusion
The minimum amplitude at which the block will separate from the plank is approximately:
A≈1.01m
The block will separate from the plank when the normal force acting on it becomes zero. This occurs when the upward acceleration of the plank due to SHM exceeds the acceleration due to gravity (g).
In SHM, the maximum acceleration (a_max) can be expressed as:
amax=ω2A
where:
- ω is the angular frequency,
- A is the amplitude of the motion.
amax>g
This leads to:
ω2A>g
The angular frequency ω is related to the period T by the formula:
ω=2πT
Given that the period T is 2 seconds, we can calculate ω:
ω=2π2=πrad/s
Substituting ω into the inequality:
π2A>g
Thus, we can express the amplitude A as:
A>gπ2
Now, substituting g (approximately 10 m/s²):
A>10π2
Calculating π2 (approximately 9.87):
A>109.87≈1.01m
The minimum amplitude at which the block will separate from the plank is approximately:
A≈1.01m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A block of mass m is resting on a piston as shown in figure which is moving vertically with a SHM of period 1s. The minimum amplitude of motion at which the block and piston separate is :

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
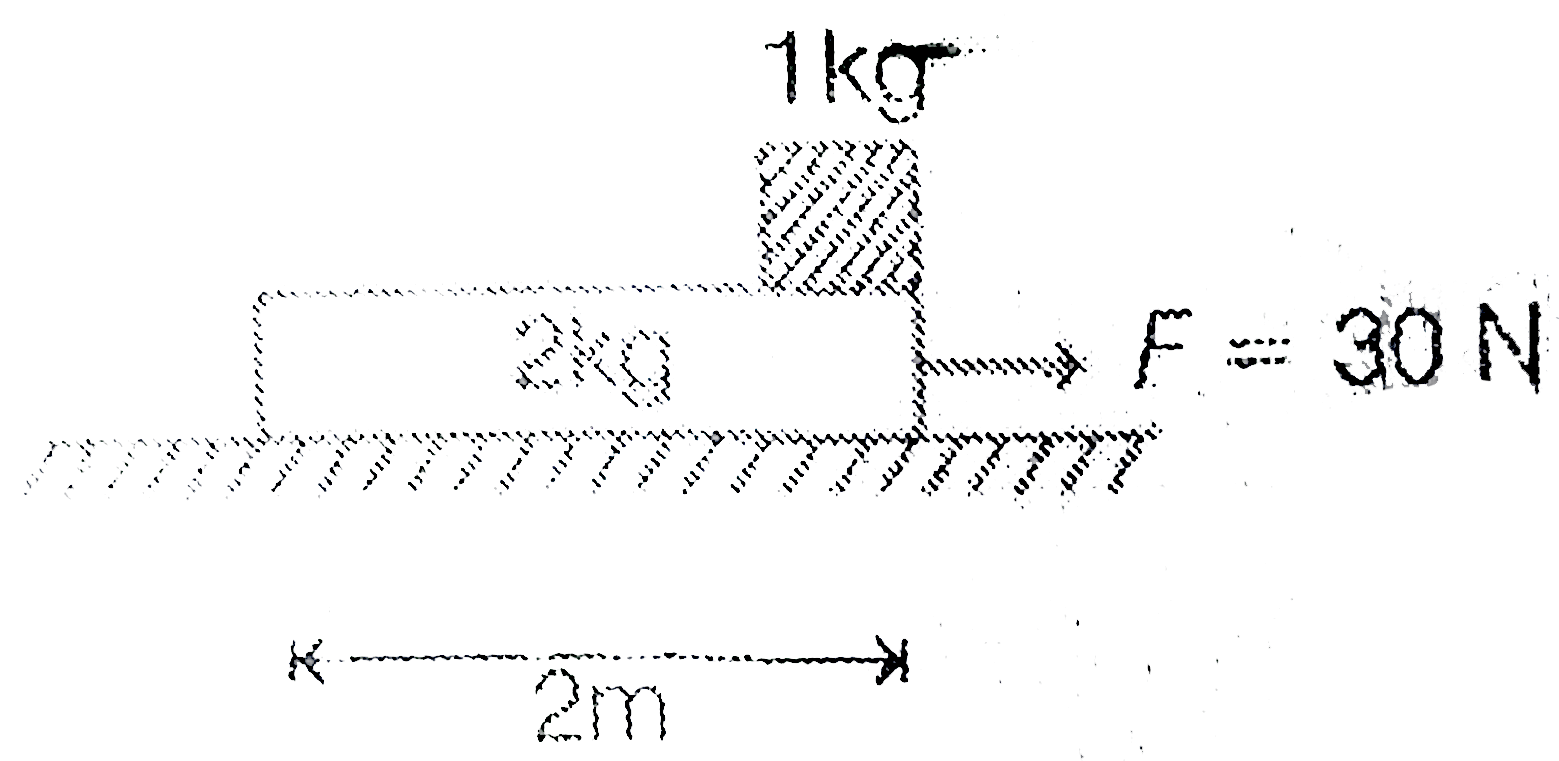
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of 2.0s in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of 2.0s in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionA horizontal platform with a small block of mass 1 kg kept on it performs vertical SHM of amplitude 1 cm. The block does not lose contact with the platform anywhere. The minimum possible time period of the platform
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View SolutionA particle of mass m is projected at an angle of 60∘ with a velocity of 20m/s relative to the ground from a plank of same mass m which is placed on smooth surface Initially Plank was at rest The minimum length of the plank for which the ball will fall on the plank itself is (g=10m/s2)

View SolutionA plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
View Solution
