In the previous problem, the displacement of the particle from the mean position corresponding to the instant mentioned is
5πm
5√3πm
10√3πm
5√32πm
The correct Answer is:B
To solve the problem of finding the displacement of a particle from the mean position in simple harmonic motion (SHM), we can follow these steps:
1. Understand the Problem: We need to find the displacement of a particle in SHM at a specific time, given that the maximum velocity (B_max) is 5 m/s.
2. Identify the Formula: The displacement x in SHM can be expressed as:
x=Acos(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- t is the time,
- ϕ is the phase constant.
3. Relate Maximum Velocity to Amplitude and Angular Frequency: The maximum velocity Bmax is given by the formula:
Bmax=Aω
Since Bmax=5m/s, we can express this as:
Aω=5
4. Determine the Angular Frequency: The angular frequency ω can be related to the period T of the motion:
ω=2πT
If we assume a time period T of 4 seconds, then:
ω=2π4=π2rad/s
5. Calculate Amplitude: Substitute ω back into the maximum velocity equation:
A⋅π2=5⟹A=5⋅2π=10πm
6. Determine the Phase Constant: If we assume a phase constant ϕ of π6 (as mentioned in the transcript), we can now substitute t=4 seconds into the displacement equation:
x=Acos(ωt+ϕ)=10πcos(π2⋅4+π6)
7. Calculate the Argument of the Cosine:
π2⋅4=2πand2π+π6=2π+π6=2π+0.5236≈2π+0.524
Since cosine is periodic with a period of 2π:
cos(2π+π6)=cos(π6)=√32
8. Final Calculation of Displacement:
x=10π⋅√32=5√3πm
Final Answer:
The displacement of the particle from the mean position at t=4 seconds is:
x=5√3πm
x=Acos(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- t is the time,
- ϕ is the phase constant.
Bmax=Aω
Since Bmax=5m/s, we can express this as:
Aω=5
ω=2πT
If we assume a time period T of 4 seconds, then:
ω=2π4=π2rad/s
A⋅π2=5⟹A=5⋅2π=10πm
x=Acos(ωt+ϕ)=10πcos(π2⋅4+π6)
π2⋅4=2πand2π+π6=2π+π6=2π+0.5236≈2π+0.524
Since cosine is periodic with a period of 2π:
cos(2π+π6)=cos(π6)=√32
x=10π⋅√32=5√3πm
The displacement of the particle from the mean position at t=4 seconds is:
x=5√3πm
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
View SolutionThe amplitude of a executing SHM is 4cm At the mean position the speed of the particle is 16cm/s The distance of the particle from the mean position at which the speed the particle becomes 8√3cm/s will be
View SolutionIn the above problem, the maximum positive displacement x is
View SolutionThe maximum displacement of a vibrating object in a medium from its mean position
View SolutionA particle is projected horizontally as shown from the rim of a large hemispherical bowl. The displacement of the particle when it strikes the bowl the first time is R. Find the velocity of the particle at that instant and the time taken.

View SolutionVelocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.
View SolutionSound wave is travellimg along positive x -direction . Displacement (y) of particles from their mean position at position x is a shown in figure . Choose the correct alternative(s).
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
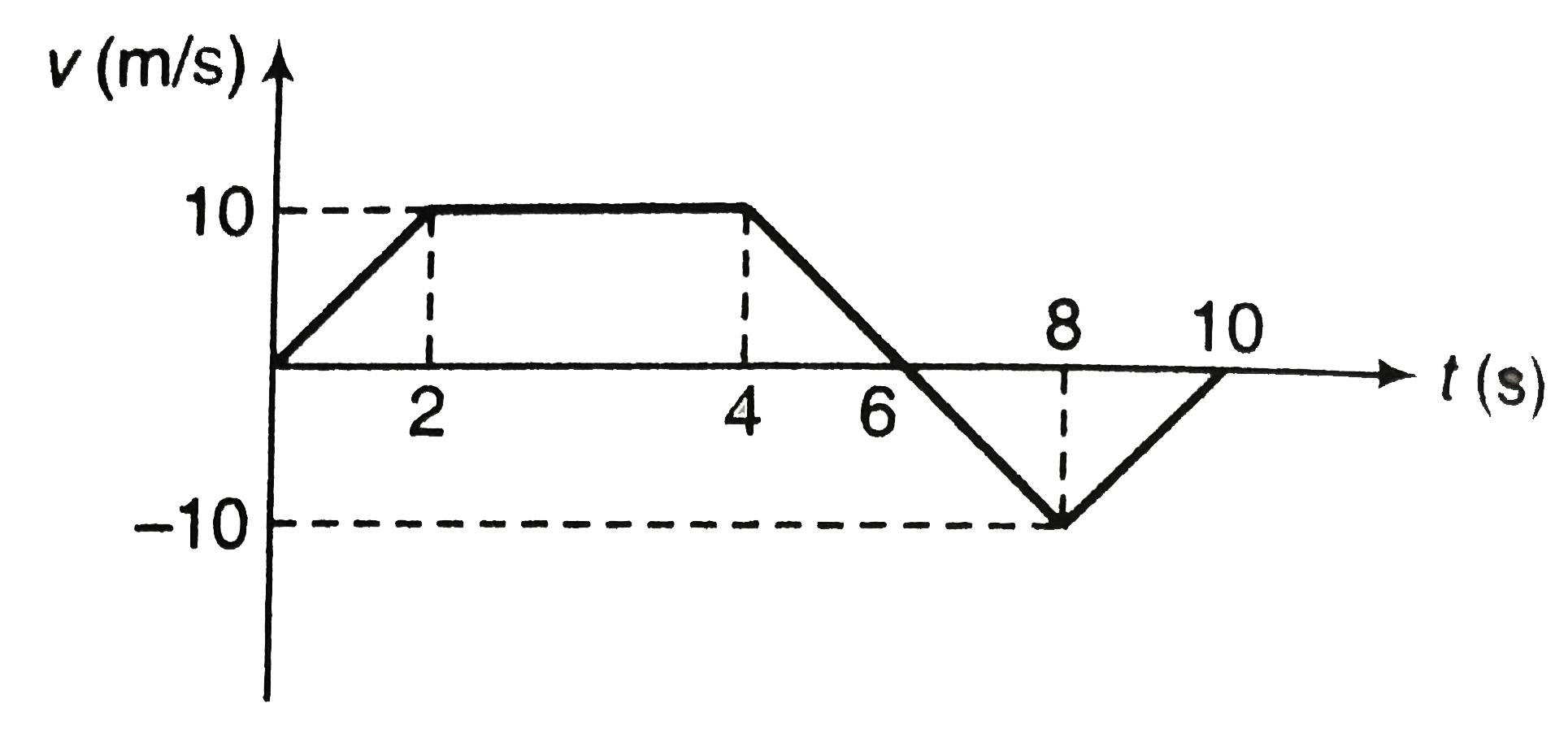
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8s
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionA particle of mass m executing SHM with angular frequency ω0 and amplitude A0, The graph of velocity of the particle with the displacement of the particle from mean position will be(ω0=1)
View Solution