Question

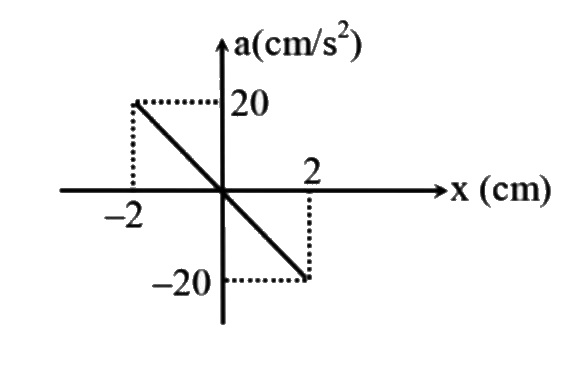
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is

Options

A. `4s^-1`
B. `((5)/(2pi))s^-1`
C. `((1)/(8pi))s^-1`
D. `((1)/(2pi))s^-1`

Answer

B

Explanation

The slope of the length is
`(F)/(x)=-(0.5)/(5)=-0.1(N)/(cm)=-10(N)/(m)`
But `F=-momega^2x` or `(F)/(x)=-momega^2`
so, `-momega^2=-10` or `momega^2=10`
or `omega^2=(10)/(m)`
`omega^2=(10)/(4xx10^-1)impliesomega=(10)/(2)=5`
`f=(omega)/(2pi)=((5)/(2pi))/(s)`