The resultant force acting on a particle executing simple harmonic motion is 4N when it is 5cm away from the centre of oscillation. Find the spring constant.
To find the spring constant k for a particle executing simple harmonic motion, we can use the formula for the force acting on the particle:
1. Understand the relationship: The force F acting on a particle in simple harmonic motion is given by Hooke's Law:
F=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
2. Identify the given values: From the problem, we know:
- The resultant force F=4N (magnitude)
- The displacement x=5cm=0.05m (convert cm to m)
3. Rearrange the formula: We can rearrange the formula to solve for the spring constant k:
k=Fx
4. Substitute the known values:
k=4N0.05m
5. Calculate k:
k=40.05=80N/m
6. Conclusion: The spring constant k is 80N/m.
F=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
- The resultant force F=4N (magnitude)
- The displacement x=5cm=0.05m (convert cm to m)
k=Fx
k=4N0.05m
k=40.05=80N/m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - worked out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
The restoing force acting on a body executing simple harmonic motion is 16 N when the body is 4 cm away from the equilibrium position. Calculate the spring constant.
View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
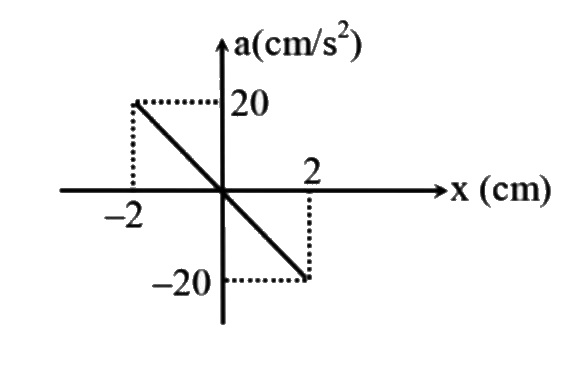
View Solution
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2πThe maximum velocity of a particle executing simple harmonic motion is v. If the amplitude is doubled and the time period of oscillation decreased to 1/3 of its original value the maximum velocity becomes
A18vB12vC6vD3v
The maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View SolutionThe total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionThe acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View Solution
