The restoing force acting on a body executing simple harmonic motion is 16 N when the body is 4 cm away from the equilibrium position. Calculate the spring constant.
To solve the problem, we need to find the spring constant k using the formula for the restoring force in simple harmonic motion. The steps are as follows:
Step 1: Understand the formula for restoring force
The restoring force F acting on a body in simple harmonic motion is given by the formula:
F=−kx
where:
- F is the restoring force,
- k is the spring constant, and
- x is the displacement from the equilibrium position.
Step 2: Identify the given values
From the problem, we know:
- The restoring force F=16N
- The displacement x=4cm
Step 3: Convert displacement to meters
Since the standard unit of displacement in physics is meters, we need to convert x from centimeters to meters:
x=4cm=4100m=0.04m
Step 4: Rearrange the formula to solve for k
We can rearrange the formula to solve for the spring constant k:
k=−Fx
Since we are interested in the magnitude of k, we can ignore the negative sign (which indicates direction).
Step 5: Substitute the values into the equation
Now, substituting the known values into the equation:
k=16N0.04m
Step 6: Calculate the spring constant
Now, perform the calculation:
k=160.04=400N/m
Final Answer
The spring constant k is:
k=400N/m
---
The restoring force F acting on a body in simple harmonic motion is given by the formula:
F=−kx
where:
- F is the restoring force,
- k is the spring constant, and
- x is the displacement from the equilibrium position.
From the problem, we know:
- The restoring force F=16N
- The displacement x=4cm
Since the standard unit of displacement in physics is meters, we need to convert x from centimeters to meters:
x=4cm=4100m=0.04m
We can rearrange the formula to solve for the spring constant k:
k=−Fx
Since we are interested in the magnitude of k, we can ignore the negative sign (which indicates direction).
Now, substituting the known values into the equation:
k=16N0.04m
Now, perform the calculation:
k=160.04=400N/m
The spring constant k is:
k=400N/m
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL SOLVED PROBLEMS
11 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS WITH ANSWER
20 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
The resultant force acting on a particle executing simple harmonic motion is 4N when it is 5cm away from the centre of oscillation. Find the spring constant.
View SolutionA horizontal spring block system of mass M executes simple harmonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
View SolutionThe total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionA particle executing harmonic motion is having velocities v1 and v2 at distances is x1 and x2 from the equilibrium position. The amplitude of the motion is
View SolutionA particle is vibrating in a simple harmonic motion with an amplitude of 4 cm . At what displacement from the equilibrium position, is its energy half potential and half kinetic
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
View SolutionThe variation of force F acting on a body moving along x - axis varies with its position (x) as shown in figure
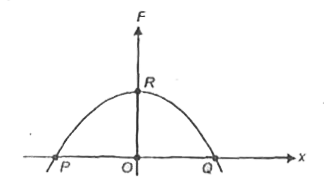
The body is in stable equilibrium stable at
View SolutionA body is vibrating in simple harmonic motion . If its acceleration in 12cms−2 at a displacement 3 cm from the mean position, then time period is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution
