Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
Let y=Asin(ωt+ϕ)
Att=0
R=Asinϕ
and dydt=Aωcosθ(ω+ϕ)
At t=0, the velocity of the partical is downwards direction i.e. v=−√gR
dydt=−√gR=A√gRcosϕ[asω=√gR]
Acosϕ=−R
tanϕ=−1⇒ϕ=3π4
Squaring and adding Eqs, (i) and (ii), A=√2R
y=√2sin(√gRr+3π4)
At y=0,sin(√gRr+3π4)=π⇒t=π4√Rg
Hence time to sross the tunnel =π2√Rg
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Solved Example
Explore 15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to reach centre of earth if it is projected into the tunnel from surface of earth with speed needed for it to escape the gravitational field to earth.
View SolutionA tunnel is made across the earth passing through its center. A ball is dropped from a height h in the tunnel. The motion will be periodic with time period::

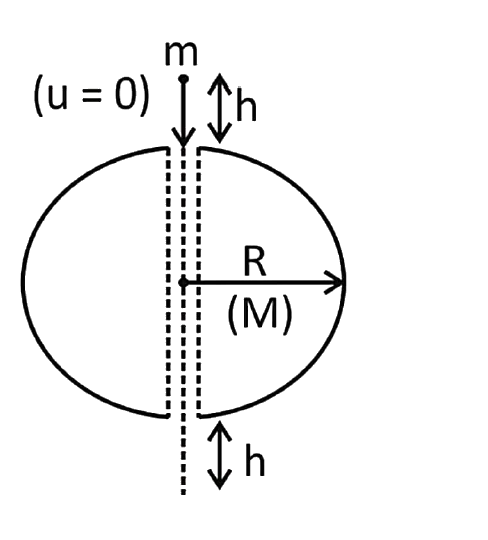
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionAssume that a frictionless tunnel is made in the earth along its diameter, a particle in projected in the tunnel from the surface of the earth with an initial speed v0=√gR, where g is the acceleration due to gravity on the earth's surface & R is the radius of the earth, if time taken by the particle to reach the centre of the earth is πn√4Rg the value of n is?
View SolutionA tunnel is dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
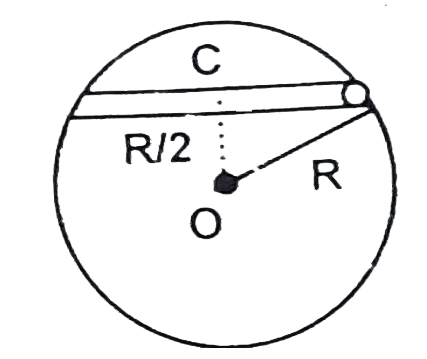
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View SolutionAssume that a tunnel is dug through earth from North pole to south pole and that the earth is a non-rotating, uniform sphere of density ρ. The gravitational force on a particle of mass m dropped into the tunnel when it reaches a distance r from the centre of earth is
View SolutionA body is projected vertically upwards with a speed of √GMR ( M is mass and R is radius of earth ) . The body will attain a height of
View Solution