Question

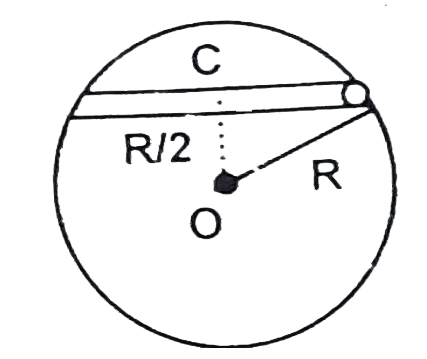
A tunnel is dug along a chord of the earth a perpendicular distance $\frac{R}{2}$ from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.

Answer

B

Explanation

To solve the problem, we need to find the force exerted by the wall of the tunnel on a particle of mass $$m$$ when it is at a distance $$x$$ from the center of the tunnel. The tunnel is dug along a chord of the Earth at a perpendicular distance $$R/2$$ from the Earth's center.

1. Understand the Geometry:
- Let \( O \) be the center of the Earth.
- The radius of the Earth is \( R \).
- The tunnel is dug at a distance \( R/2 \) from the center, which means the tunnel is horizontal and at a depth of \( R/2 \) from the surface.

2. Determine the Distance from the Center of the Earth:
- If \( x \) is the distance from the center of the tunnel to the mass \( m \), the distance \( d \) from the center of the Earth to the mass \( m \) can be expressed using the Pythagorean theorem:
\( d = \sqrt{x^2 + \left(\frac{R}{2}\right)^2} = \sqrt{x^2 + \frac{R^2}{4}} \)

3. Calculate the Mass of the Earth and the Mass Enclosed:
- The mass of the Earth \( M \) can be given by:
\( M = \frac{4}{3} \pi R^3 \rho \)
- The mass \( M' \) enclosed within the radius \( d \) is:
\( M' = \frac{4}{3} \pi d^3 \rho \)

4. Express the Ratio of Masses:
- The ratio of the mass \( M' \) to the mass \( M \) is:
\( \frac{M'}{M} = \frac{d^3}{R^3} \)

5. Calculate the Gravitational Force:
- The gravitational force \( F \) acting on the mass \( m \) due to the mass \( M' \) is given by:
\( F = \frac{G M' m}{d^2} \)
- Substituting \( M' \):
\( F = \frac{G \left(\frac{4}{3} \pi d^3 \rho\right) m}{d^2} = \frac{4 \pi G \rho m d}{3} \)

6. Substituting for \( d \):
- Substitute \( d = \sqrt{x^2 + \frac{R^2}{4}} \):
\( F = \frac{4 \pi G \rho m}{3} \sqrt{x^2 + \frac{R^2}{4}} \)

7. Normal Force Exerted by the Wall:
- Since the wall is frictionless, the normal force \( N \) exerted by the wall on the mass \( m \) is equal to the gravitational force calculated:
\( N = F = \frac{4 \pi G \rho m}{3} \sqrt{x^2 + \frac{R^2}{4}} \)

Final Result:
The force exerted by the wall on a particle of mass \( m \) when it is at a distance \( x \) from the center of the tunnel is:
\( N = \frac{4 \pi G \rho m}{3} \sqrt{x^2 + \frac{R^2}{4}} \)