A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

The correct Answer is:A, B
At P1 gravitatioN/Al field due to sphere M
=GM(3a+a)2=GM16a2
ATP2 GravitatioN/Al field is due to sphere and shell
=(GM)/((a+4a+a)^2) (GM)/((4+a)^2)<br>=(GM)/(36a^2)+(GM)/(25a^2)<br>=(GM)/a^2(1/36+1/25)e<br>GMa2(25+36900)=(61900)GMa2

Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -2
6 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer
11 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
Similar Questions
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
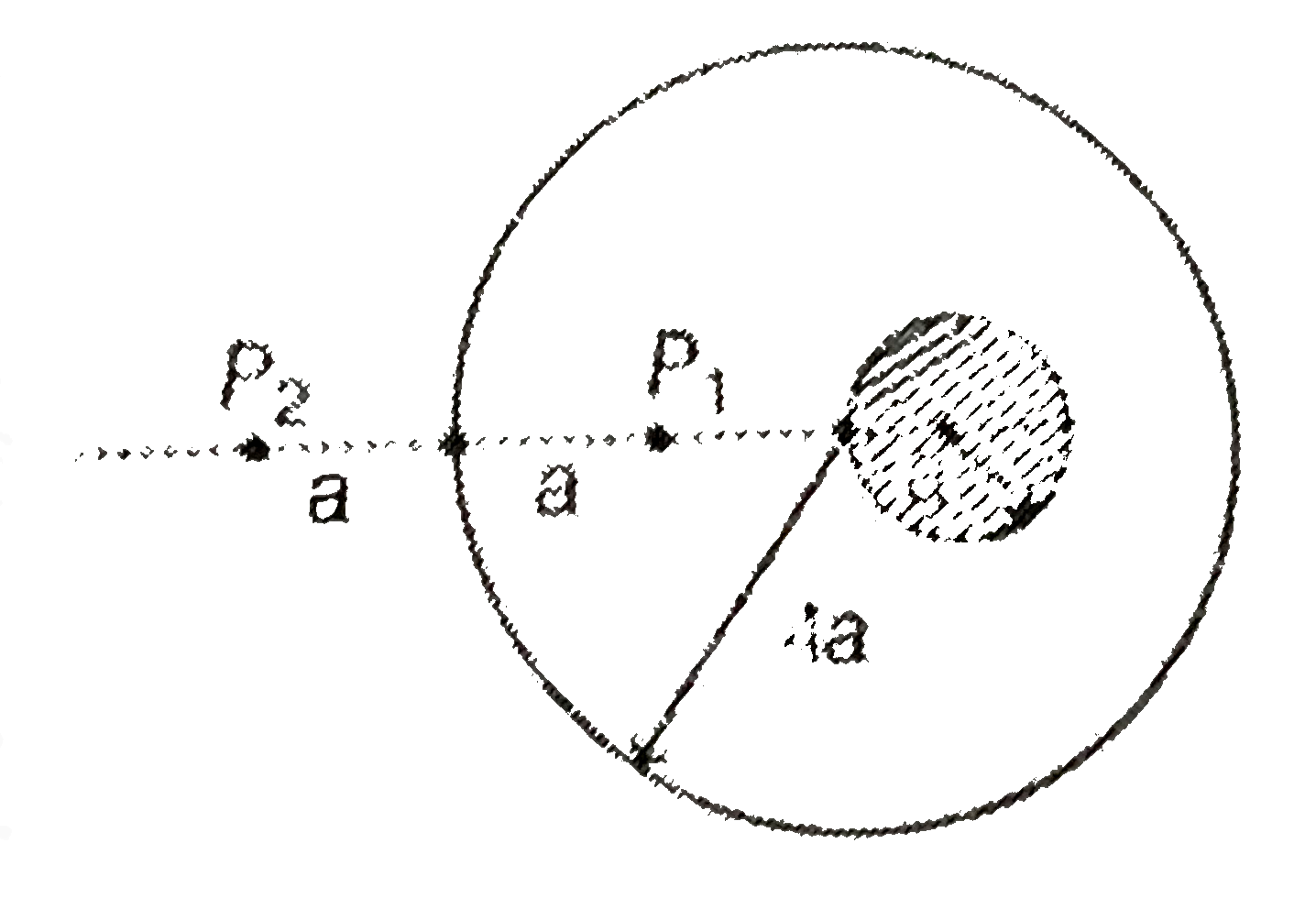
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View Solution
Knowledge Check
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMRA uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
A solid sphere of radius a and mass m is surrounded by cocentric spherical shell of thickness 2a and mass 2m the gravitational field at a distance 3a from their centres is
View SolutionA uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass is kept at a distance x(>R) in the region bounded by spheres as shown in the figure . The net gravitational force on the particle is

View SolutionConsider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution
