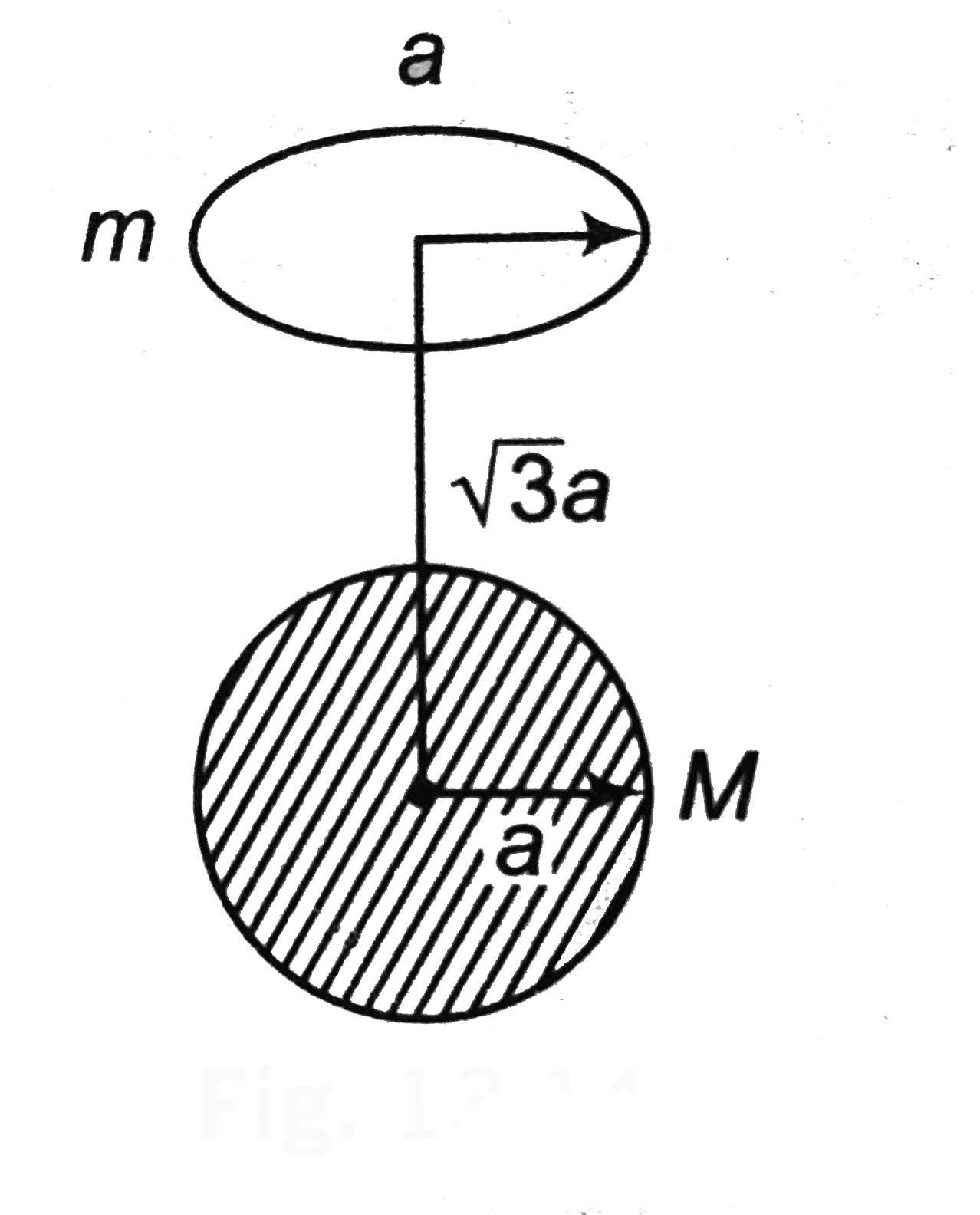
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
To find the gravitational force exerted by the sphere on the ring, we can follow these steps:
Step 1: Understand the Configuration
We have a uniform ring of mass m and radius a positioned directly above a uniform sphere of mass M and radius a. The distance between the center of the ring and the center of the sphere is given as √3a.
Step 2: Treat the Sphere as a Point Mass
For the purpose of calculating the gravitational force, we can treat the uniform sphere as a point mass located at its center. This is valid because the gravitational force exerted by a uniform sphere can be treated as if all its mass were concentrated at its center.
Step 3: Calculate the Gravitational Field Due to the Ring
The gravitational field E at a distance r from the center of the ring can be expressed as:
E=GMa2+r2⋅r(a2+r2)3/2
where G is the gravitational constant, M is the mass of the sphere, a is the radius of the ring, and r is the distance from the center of the ring to the center of the sphere.
Step 4: Substitute the Values
In our case, r=√3a and a=a. Thus, we substitute these values into the equation:
E=GMa2+(√3a)2⋅√3a(a2+3a2)3/2
This simplifies to:
E=GM4a2⋅√3a(4a2)3/2
Step 5: Simplify the Expression
Now we simplify the expression:
E=GM⋅√3a4a2⋅8a3=√3GM32a2
Step 6: Calculate the Gravitational Force
The gravitational force F exerted by the sphere on the ring can be calculated using the formula:
F=m⋅E
Substituting the expression for E:
F=m⋅√3GM32a2
Final Answer
Thus, the gravitational force exerted by the sphere on the ring is:
F=√3GmM32a2
We have a uniform ring of mass m and radius a positioned directly above a uniform sphere of mass M and radius a. The distance between the center of the ring and the center of the sphere is given as √3a.
For the purpose of calculating the gravitational force, we can treat the uniform sphere as a point mass located at its center. This is valid because the gravitational force exerted by a uniform sphere can be treated as if all its mass were concentrated at its center.
The gravitational field E at a distance r from the center of the ring can be expressed as:
E=GMa2+r2⋅r(a2+r2)3/2
where G is the gravitational constant, M is the mass of the sphere, a is the radius of the ring, and r is the distance from the center of the ring to the center of the sphere.
In our case, r=√3a and a=a. Thus, we substitute these values into the equation:
E=GMa2+(√3a)2⋅√3a(a2+3a2)3/2
This simplifies to:
E=GM4a2⋅√3a(4a2)3/2
Now we simplify the expression:
E=GM⋅√3a4a2⋅8a3=√3GM32a2
The gravitational force F exerted by the sphere on the ring can be calculated using the formula:
F=m⋅E
Substituting the expression for E:
F=m⋅√3GM32a2
Thus, the gravitational force exerted by the sphere on the ring is:
F=√3GmM32a2
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -116videos
GRAVITATION
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -26videos
GRAVITATION
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers18videos
GRAVITATION
- BOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer11videos
FRICTION
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 26videos
HEAT AND TEMPERATURE
Similar Questions
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionFor a uniform ring of mass M and radius R at its centre
View Solution
Knowledge Check
- Question 1 - Select One
A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 View Solution
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
 View Solution
View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View Solution_E01_017_Q01.png)
A spherical cave of radius R/2 was carved out from a uniform sphere of radius R and original mass M. the center of the cave is at R/2 from the center of the large sphere. Point P is at a distance 2R from the center the large sphere and on the joing line of the two centers. the gravitational field strength g at point P isView SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.
 View Solution
View Solution
