A circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
√GMa
√GM2a(mM)
√GM2a(Mm)
√GMa(MM+m)
To solve the problem, we need to find the velocity with which the particle of mass m passes through the center of the circular ring after being released from rest at a distance of √3a from the center of the ring.
1. Understanding the Setup:
- We have a circular ring of mass M and radius a.
- A small particle of mass m is placed on the axis of the ring at a distance √3a from the center of the ring.
2. Initial Conditions:
- The particle is released from rest, which means its initial velocity (v∈itial) is 0.
- The potential energy at the initial position (when the particle is at √3a) needs to be calculated.
3. Potential Energy Calculation:
- The gravitational potential energy (U) due to the ring at a distance r from its center is given by:
\(
U = -\frac{GMm}{r}
\)
- Initially, the distance from the particle to the ring is 2a (the distance from the center of the ring to the particle is √3a, and the radius of the ring is a, so the total distance is √3a+a=2a).
- Therefore, the initial potential energy (U_initial) when the particle is at √3a is:
\(
U_{initial} = -\frac{GMm}{2a}
\)
4. Final Conditions:
- When the particle passes through the center of the ring, it is at a distance a from the ring.
- The final potential energy (U_final) when the particle is at the center of the ring is:
\(
U_{final} = -\frac{GMm}{a}
\)
5. Change in Potential Energy:
- The change in potential energy (ΔU) as the particle moves from its initial position to the center of the ring is:
\(
\Delta U = U_{final} - U_{initial} = \left(-\frac{GMm}{a}\right) - \left(-\frac{GMm}{2a}\right)
\)
- Simplifying this gives:
\(
\Delta U = -\frac{GMm}{a} + \frac{GMm}{2a} = -\frac{GMm}{2a}
\)
6. Conservation of Energy:
- According to the conservation of mechanical energy:
\(
\Delta K + \Delta U = 0
\)
- The change in kinetic energy (ΔK) is given by:
\(
\Delta K = K_{final} - K_{initial} = \frac{1}{2}mv^2 - 0 = \frac{1}{2}mv^2
\)
- Setting the change in kinetic energy equal to the negative change in potential energy:
\(
\frac{1}{2}mv^2 = \frac{GMm}{2a}
\)
7. Solving for Final Velocity:
- Canceling m from both sides (assuming m is not zero):
\(
\frac{1}{2}v^2 = \frac{GM}{2a}
\)
- Multiplying both sides by 2:
\(
v^2 = \frac{GM}{a}
\)
- Taking the square root gives:
\(
v = \sqrt{\frac{GM}{a}}
\)
Final Answer:
The velocity with which the particle passes through the center of the ring is:
\(
v = \sqrt{\frac{GM}{a}}
\)
- We have a circular ring of mass M and radius a.
- A small particle of mass m is placed on the axis of the ring at a distance √3a from the center of the ring.
- The particle is released from rest, which means its initial velocity (v∈itial) is 0.
- The potential energy at the initial position (when the particle is at √3a) needs to be calculated.
- The gravitational potential energy (U) due to the ring at a distance r from its center is given by:
\(
U = -\frac{GMm}{r}
\)
- Initially, the distance from the particle to the ring is 2a (the distance from the center of the ring to the particle is √3a, and the radius of the ring is a, so the total distance is √3a+a=2a).
- Therefore, the initial potential energy (U_initial) when the particle is at √3a is:
\(
U_{initial} = -\frac{GMm}{2a}
\)
- When the particle passes through the center of the ring, it is at a distance a from the ring.
- The final potential energy (U_final) when the particle is at the center of the ring is:
\(
U_{final} = -\frac{GMm}{a}
\)
- The change in potential energy (ΔU) as the particle moves from its initial position to the center of the ring is:
\(
\Delta U = U_{final} - U_{initial} = \left(-\frac{GMm}{a}\right) - \left(-\frac{GMm}{2a}\right)
\)
- Simplifying this gives:
\(
\Delta U = -\frac{GMm}{a} + \frac{GMm}{2a} = -\frac{GMm}{2a}
\)
- According to the conservation of mechanical energy:
\(
\Delta K + \Delta U = 0
\)
- The change in kinetic energy (ΔK) is given by:
\(
\Delta K = K_{final} - K_{initial} = \frac{1}{2}mv^2 - 0 = \frac{1}{2}mv^2
\)
- Setting the change in kinetic energy equal to the negative change in potential energy:
\(
\frac{1}{2}mv^2 = \frac{GMm}{2a}
\)
- Canceling m from both sides (assuming m is not zero):
\(
\frac{1}{2}v^2 = \frac{GM}{2a}
\)
- Multiplying both sides by 2:
\(
v^2 = \frac{GM}{a}
\)
- Taking the square root gives:
\(
v = \sqrt{\frac{GM}{a}}
\)
The velocity with which the particle passes through the center of the ring is:
\(
v = \sqrt{\frac{GM}{a}}
\)
Topper's Solved these Questions
Similar Questions
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution
Knowledge Check
A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
A ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View Solution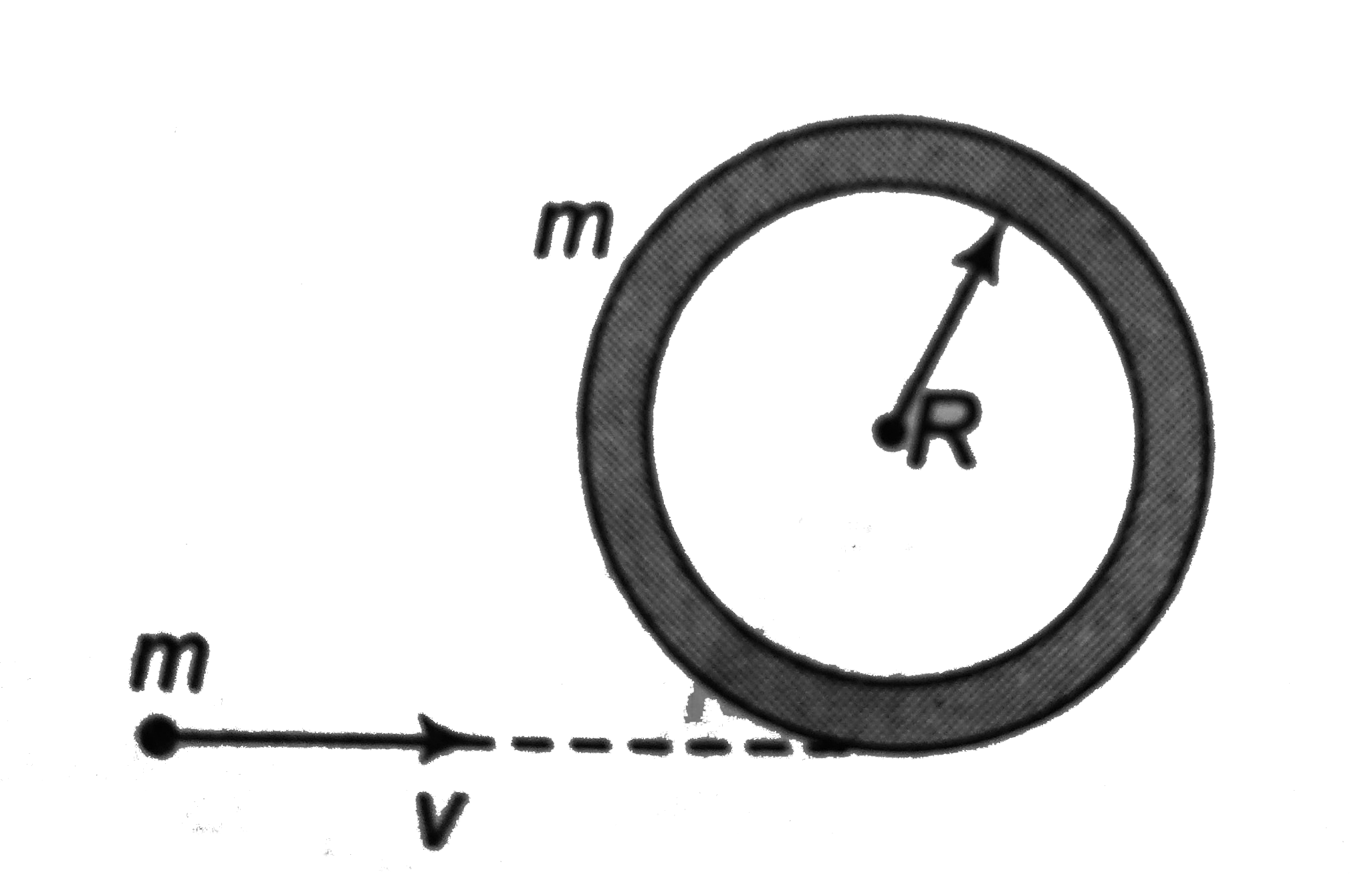
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2√3 m from the centre.
View Solution

