Two simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if the vibrational energy of both is same which is correct?
Amplitude of B greater than A
Amplitude of B smaller than A
Amplitudes will be same
none of these
The correct Answer is:B
Step by step video & image solution for Two simple pendulum first of bob mass M_(1) and length L_(1) second of bob mass M_(2) and length L_(2) M_(1) = M_(2) and L_(1) = 2L_(2). if the vibrational energy of both is same which is correct? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type3videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
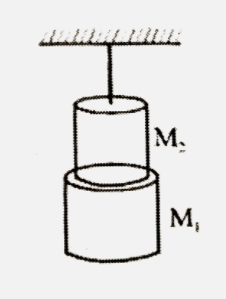
The length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
 View Solution
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionIf the direction cosines of two lines are l1,m1,n1 and l2,m2,n2, then find the direction cosine of a line perpendicular to these lines.
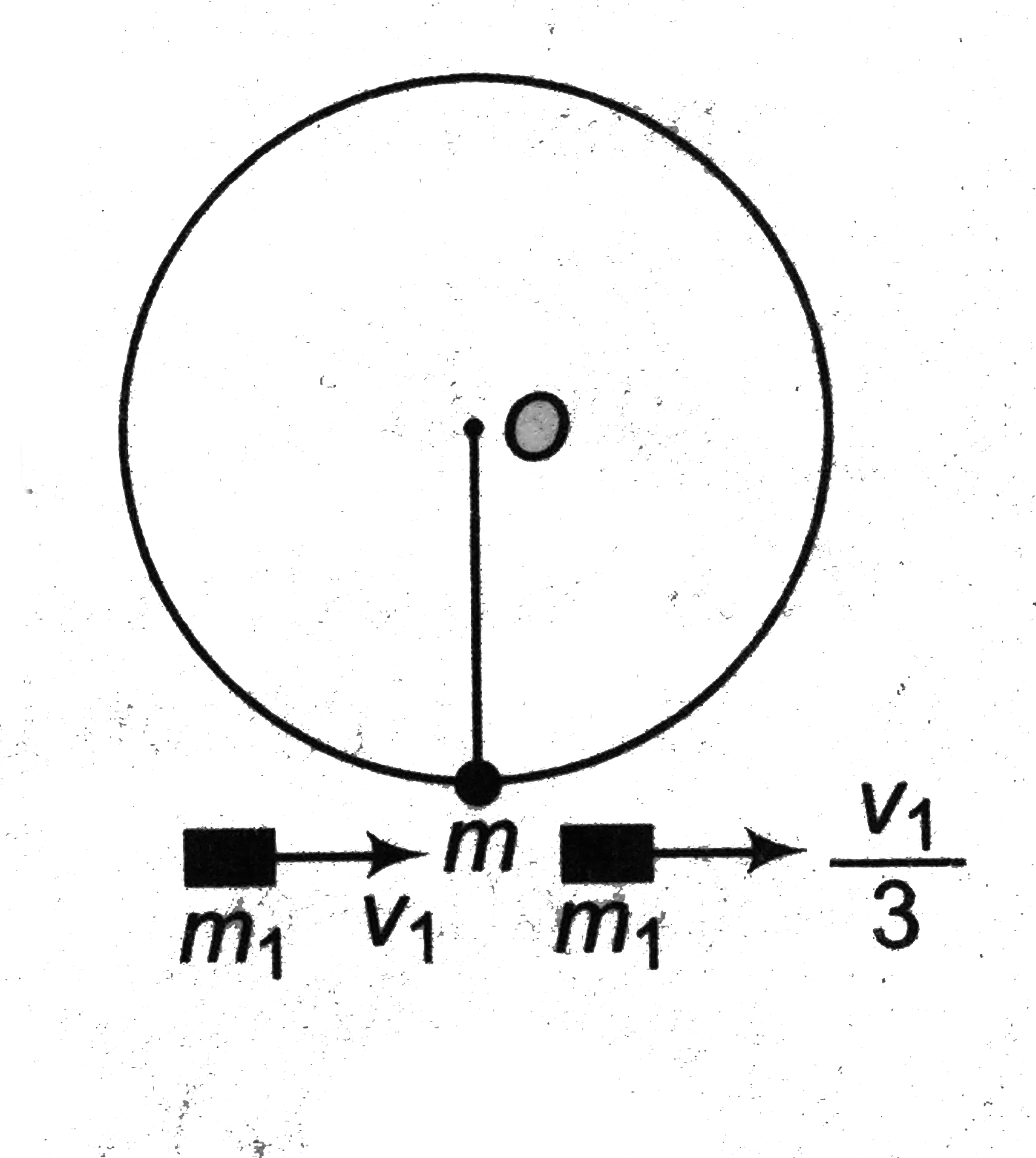
View SolutionA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
View SolutionA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
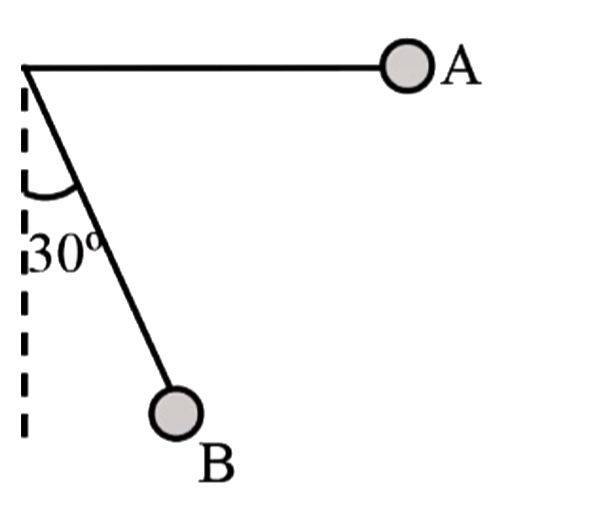
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
 View Solution
View SolutionA simple pendulum of length 1 m has a wooden bob of mass 1 kg. It is struck by a bullet of mass 10−2 kg moving with a speed of 2×102ms−1. The height to which the bob rises before swinging back is (Take g=10ms−2)
View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
View SolutionIf <l1,m1,n1>and<l2,m2,n2> be the direction cosines of two lines L1andL2 respectively. If the angle between them is θ, the cosθ=?
View SolutionA pendulum comsists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1 and it emerges from the bob with speed v13. The bob just completes motion along a vertical circle. Then v1 is
 View Solution
View Solution


