Figure. Shows two long wires carrying equal currents I1andI2 flowing in opposite directions. Which of the arrows labeled A to D correctely represents the direction of the magnetic field due to the wires at a point located at an equal distance d from each wire?
A
B
C
D
The correct Answer is:B
To solve the problem of determining the direction of the magnetic field at a point equidistant from two long wires carrying equal currents in opposite directions, we can follow these steps:
Step 1: Understand the Direction of Magnetic Field
The magnetic field around a long straight wire carrying current can be determined using the right-hand rule. If you point your thumb in the direction of the current, your fingers will curl in the direction of the magnetic field lines.
Step 2: Apply the Right-Hand Rule to Each Wire
1. For Wire 1 (Current I1):
- If the current is flowing upwards, point your right thumb upwards. Your fingers will curl around the wire, indicating that the magnetic field at a point to the right of the wire will be directed into the page (or screen).
2. For Wire 2 (Current I2):
- If the current is flowing downwards, point your right thumb downwards. Your fingers will curl around the wire, indicating that the magnetic field at a point to the right of this wire will be directed out of the page (or screen).
Step 3: Determine the Resultant Magnetic Field at the Point
At the point equidistant from both wires:
- The magnetic field due to Wire 1 (I1) is directed into the page.
- The magnetic field due to Wire 2 (I2) is directed out of the page.
Since both magnetic fields are equal in magnitude but opposite in direction, they will cancel each other out at the point equidistant from the two wires.
Step 4: Conclusion
Since the magnetic fields due to the two wires cancel each other out at the point of interest, the net magnetic field at that point is zero. Therefore, none of the arrows labeled A to D would correctly represent a non-zero magnetic field at that point.
Final Answer
The correct answer is that the net magnetic field at the point is zero due to cancellation.
---
The magnetic field around a long straight wire carrying current can be determined using the right-hand rule. If you point your thumb in the direction of the current, your fingers will curl in the direction of the magnetic field lines.
1. For Wire 1 (Current I1):
- If the current is flowing upwards, point your right thumb upwards. Your fingers will curl around the wire, indicating that the magnetic field at a point to the right of the wire will be directed into the page (or screen).
2. For Wire 2 (Current I2):
- If the current is flowing downwards, point your right thumb downwards. Your fingers will curl around the wire, indicating that the magnetic field at a point to the right of this wire will be directed out of the page (or screen).
At the point equidistant from both wires:
- The magnetic field due to Wire 1 (I1) is directed into the page.
- The magnetic field due to Wire 2 (I2) is directed out of the page.
Since the magnetic fields due to the two wires cancel each other out at the point of interest, the net magnetic field at that point is zero. Therefore, none of the arrows labeled A to D would correctly represent a non-zero magnetic field at that point.
The correct answer is that the net magnetic field at the point is zero due to cancellation.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
An electric current flows in a wire from north to south.
What will be the direction of the magnetic field due to this wire at a point.
View SolutionTwo long wire AB abd CD carry currents i1 and i2 in the direactions show in figure

View SolutionThe two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View SolutionA non - popular loop of conducting wire carrying a current I is placed as shown in the figure . Each of the straighrt sections of the loop is of the length 2a. The magnetic field due to this loop at the point P(a,0,a) points in the direction

View SolutionTwo parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionEach of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionTwo long, straight wires, one above the other, are separated by a distance 2a and are parallel to the x-axis. Let the y-axis be in the plane of the wires in the direction form the lower wire to the upper wire. Each wire carries current I in the +x-direction. What are the magnitude and direction of the net magnetic field of the two wires at a point in the plane of wires:
(a) midway between them?
(b) at a distance a above the upper wire?
(c) at a distance a below the lower wire?
View SolutionTwo long wires carrying same currents in opposite directions are placed at separation D as shown.Predict variation of magnetic field as one moves from the point O and A
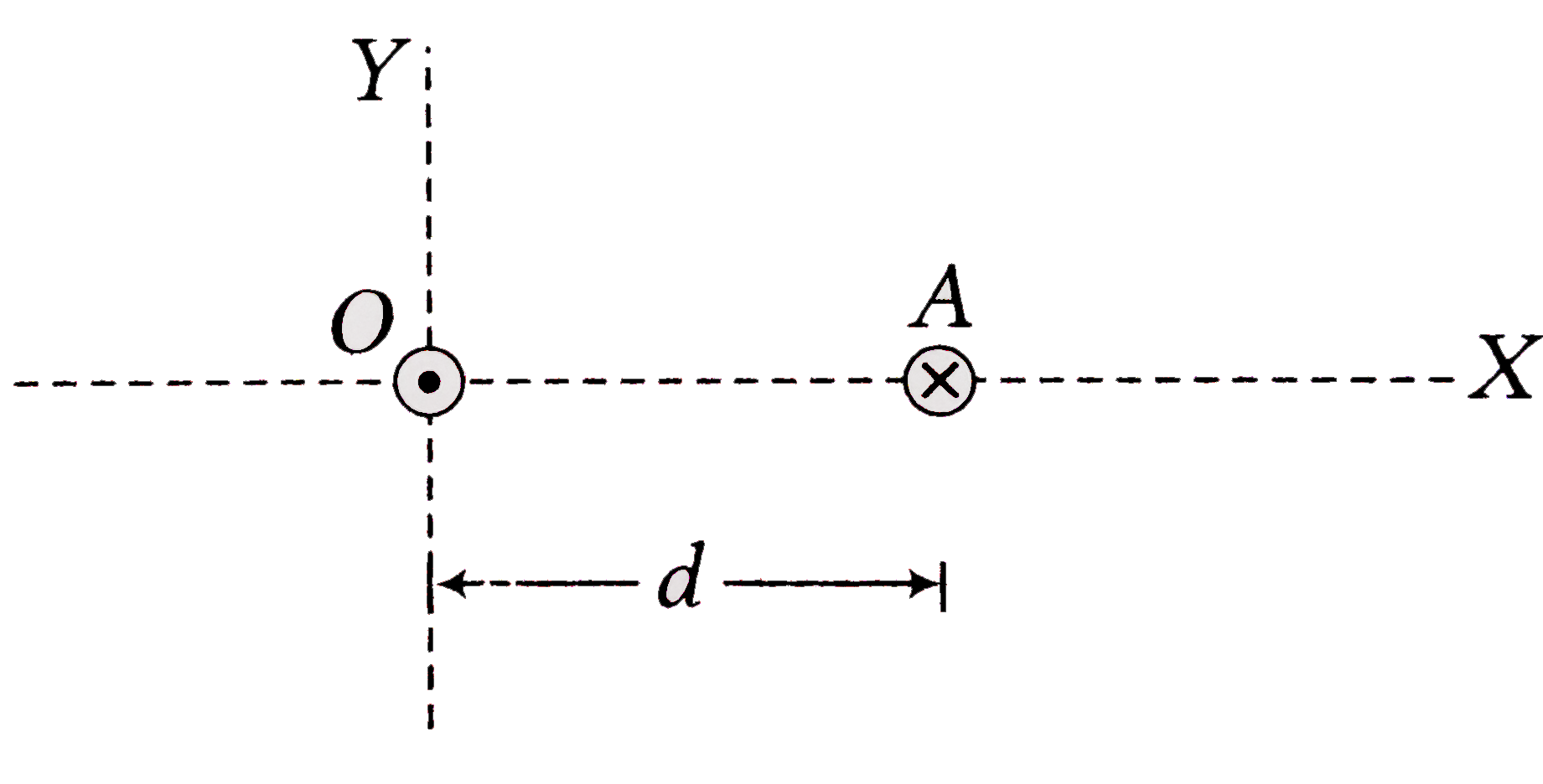
View Solution
