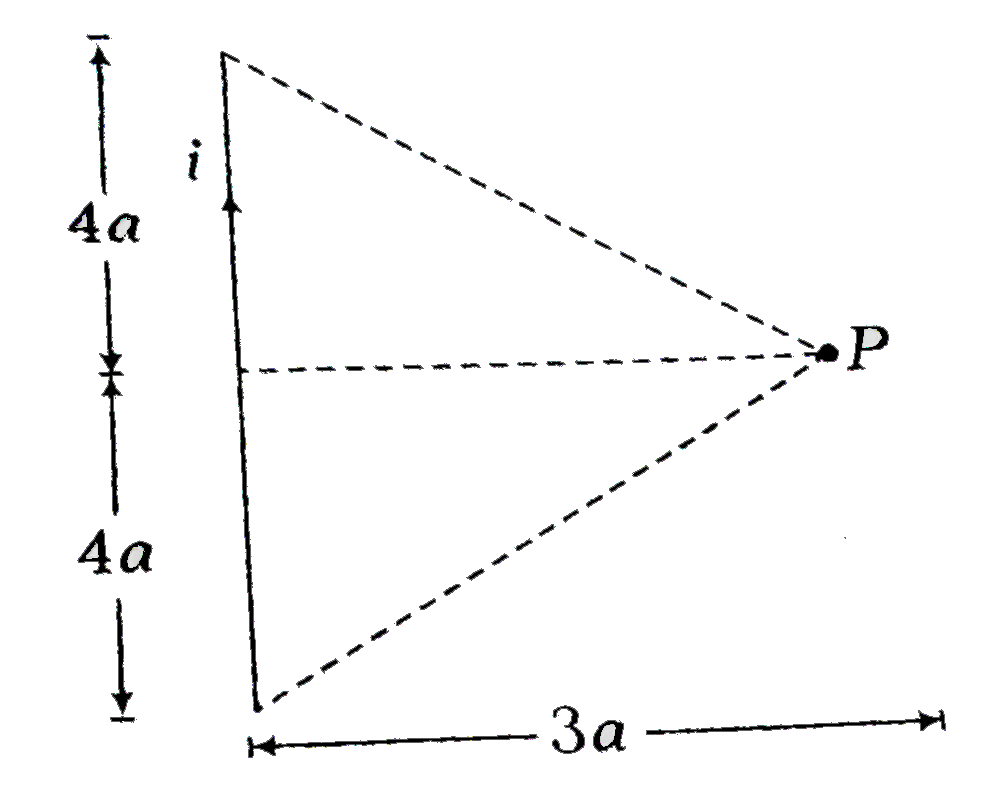
Find the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

B=μ0I4πR[sinθ1+sinθ2]
Here, θ1=−30∘,θ2=60∘. Putting these values, we get
B=μ0I4πR[−1/2+√3/2]=μ0I8πR(√3−1)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Solved Example
Explore 20 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.1
Explore 35 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
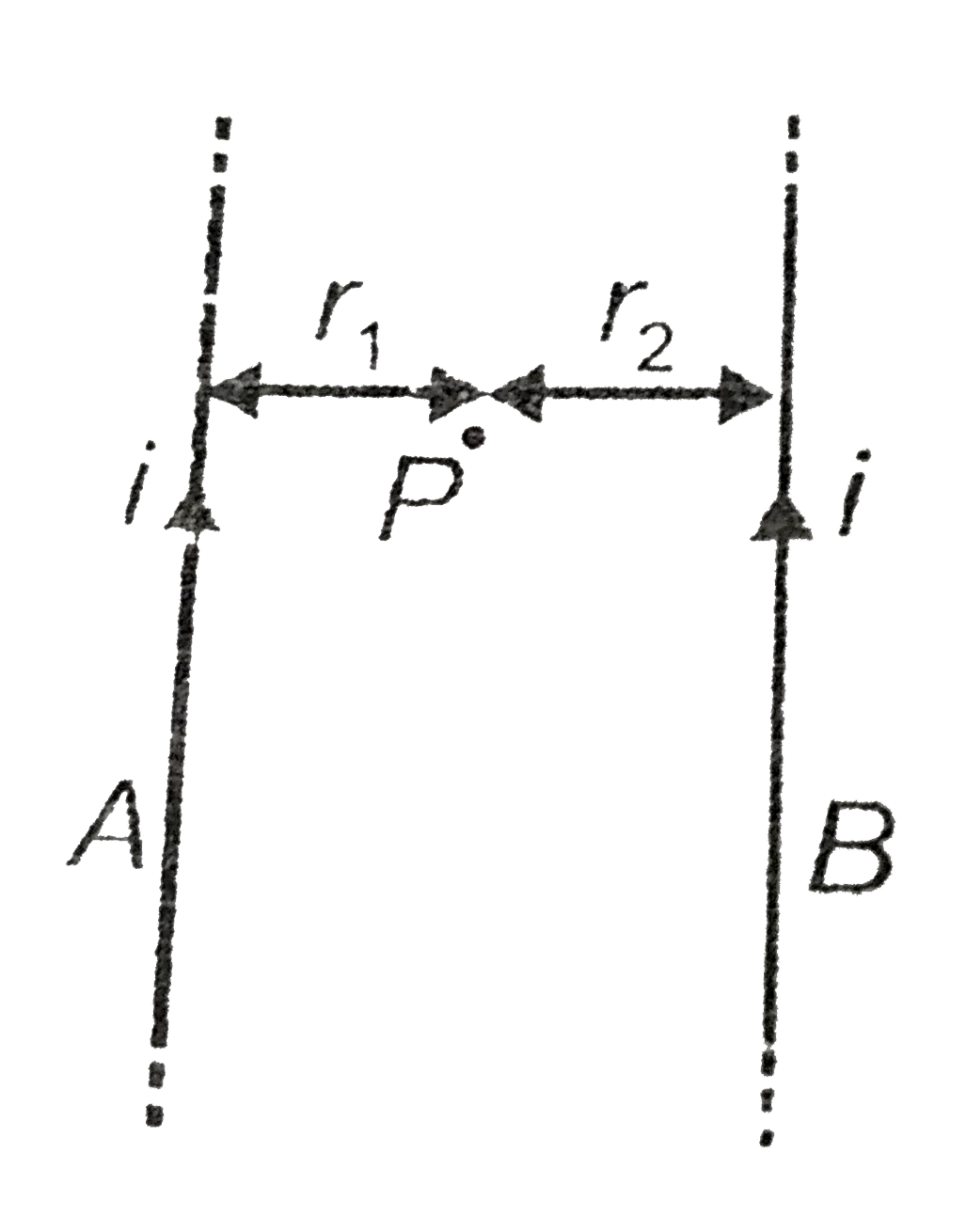
Find the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2
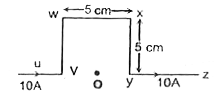
View SolutionFind the magnitude and direction of magnetic field at point O in the following case

View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
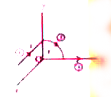
View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases

View SolutionFind magnetic field at C by the system of current carrying wire.
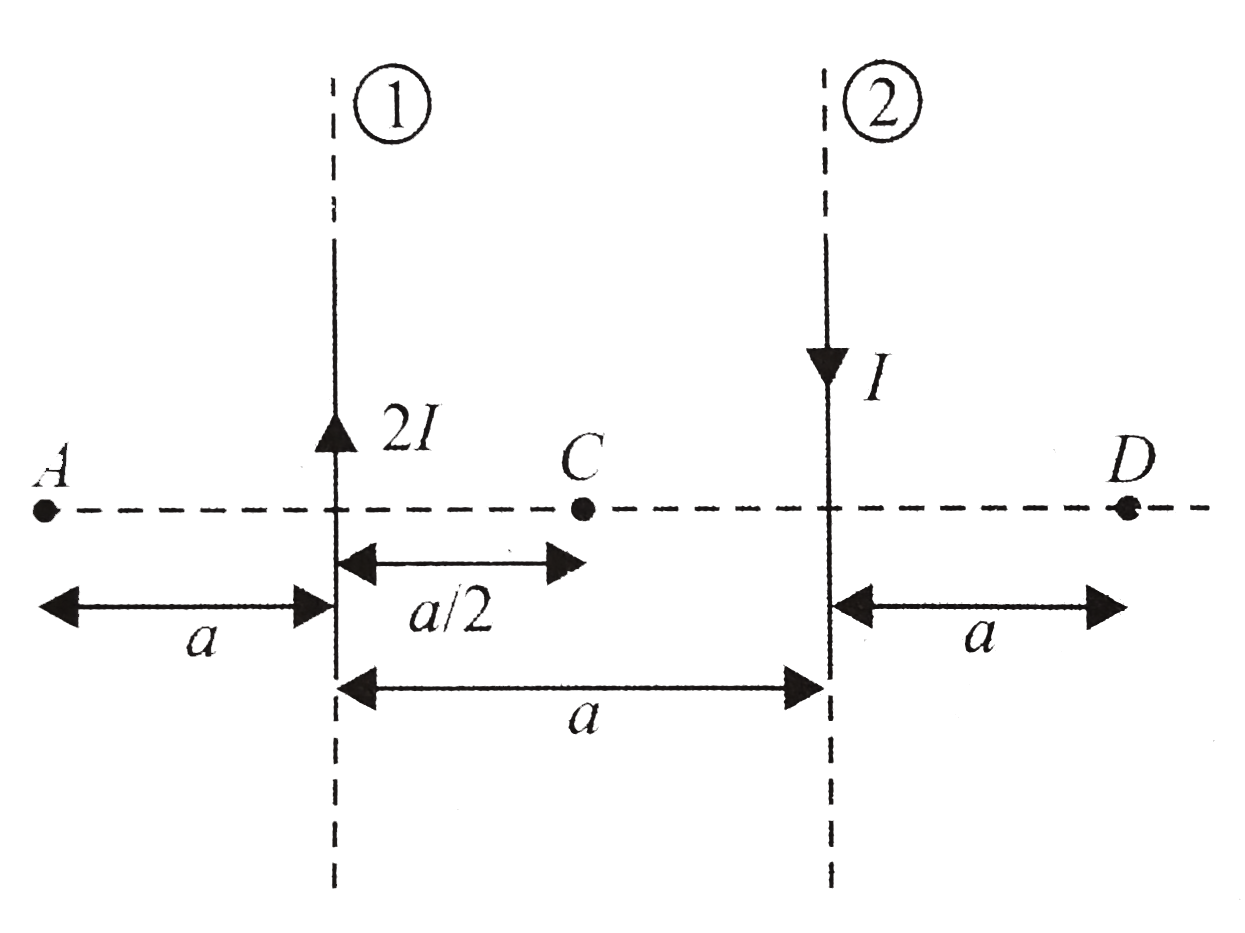

View SolutionFind the magnetic field at P due to the arrangement shown
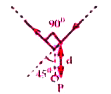
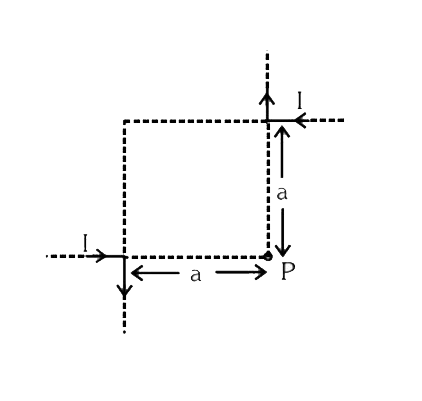
View SolutionMagnetic field at point 'P' due to given current distribution :-
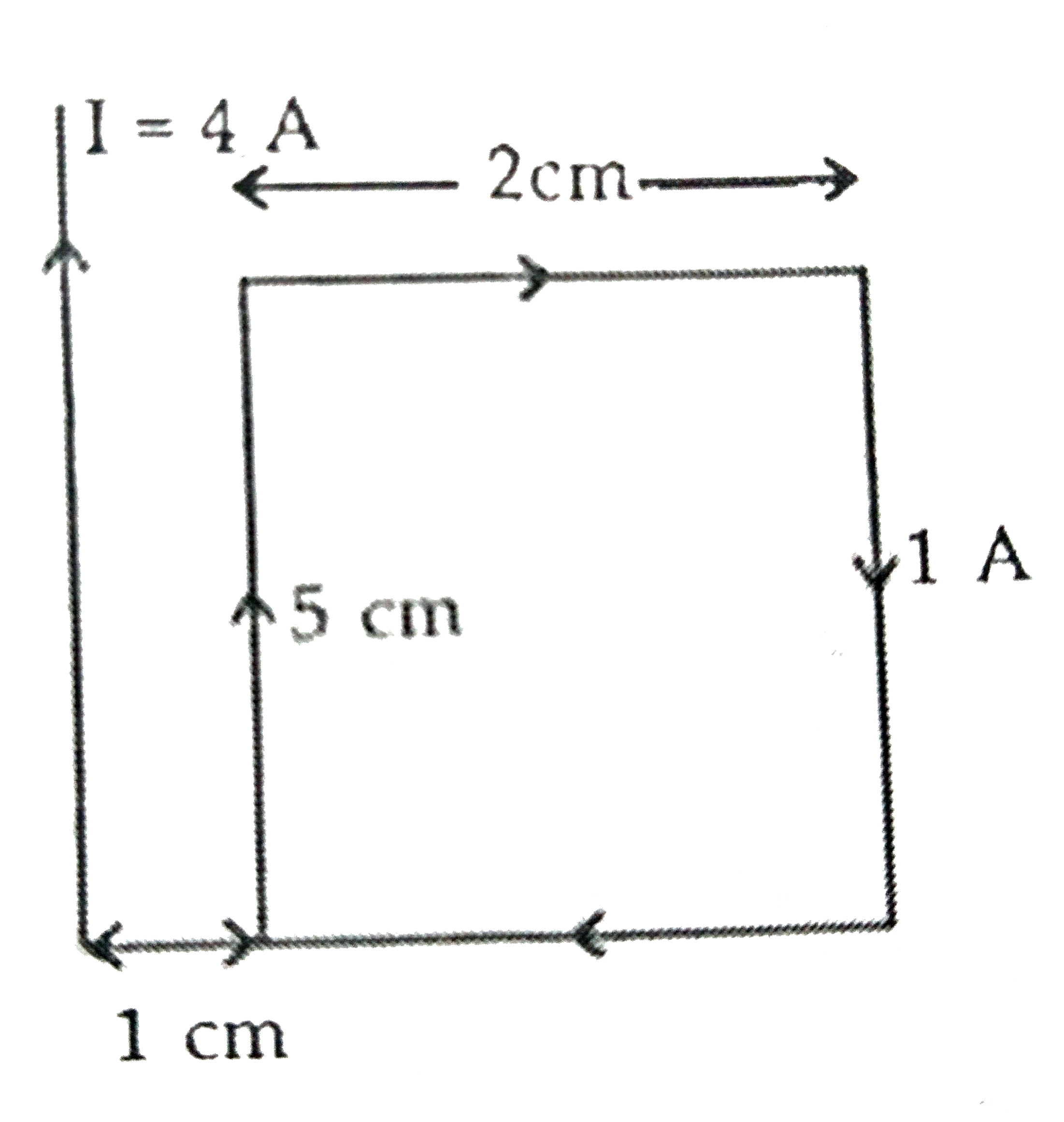
View SolutionA rectangular loop of wire of size 2cm×5cm carries a steady current of 1A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the end
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View Solution
