A coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as

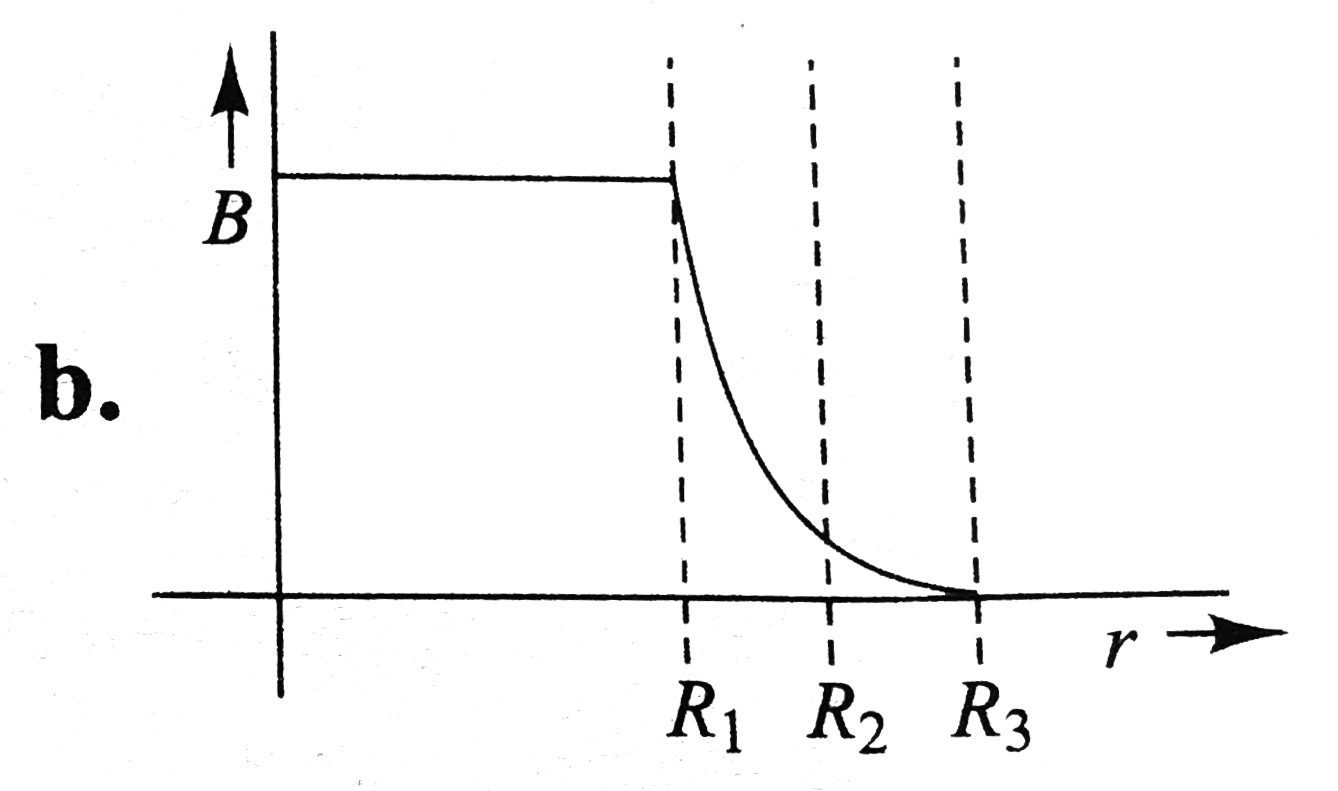

The correct Answer is:C
To solve the problem of the variation of the magnetic field with distance from the axis in a coaxial cable with two conductors carrying equal currents in opposite directions, we will apply Ampere's circuital law step by step.
1. Understanding the Configuration:
- We have an inner solid conductor with radius R1.
- The outer conductor is hollow, with an inner radius R2 and outer radius R3.
- Both conductors carry equal currents I in opposite directions.
2. Applying Ampere's Circuital Law:
- Ampere's law states that the line integral of the magnetic field B around a closed loop is equal to μ0 times the current enclosed by that loop:
∮B⋅dl=μ0Ienc
3. Case 1: Inside the Inner Conductor (r<R1):
- For a circular loop of radius r inside the inner conductor, the enclosed current Ienc can be calculated using the ratio of areas:
Ienc=I⋅AloopAtotal=I⋅πr2πR21=I⋅r2R21
- Applying Ampere's law:
B⋅2πr=μ0I⋅r2R21
- Solving for B:
B=μ0Ir2πR21
- This shows that B is directly proportional to r for r<R1.
4. Case 2: Between the Conductors (R1<r<R2):
- For a loop in the air gap between the inner and outer conductors, the enclosed current is just I (the current in the inner conductor):
B⋅2πr=μ0I
- Solving for B:
B=μ0I2πr
- This indicates that B is inversely proportional to r for R1<r<R2.
5. Case 3: Outside the Outer Conductor (r>R3):
- For r>R3, the total current enclosed is zero because the currents in the inner and outer conductors cancel each other out:
B⋅2πr=0⟹B=0
6. Graphing the Magnetic Field:
- For r<R1: B increases linearly with r.
- For R1<r<R2: B decreases inversely with r.
- For r>R3: B=0.
Conclusion:
The variation of the magnetic field with distance from the axis can be summarized as:
- Increases linearly for r<R1
- Decreases inversely for R1<r<R2
- Becomes zero for r>R3
Thus, the best plot for the variation of the magnetic field with distance from the axis corresponds to option C.
- We have an inner solid conductor with radius R1.
- The outer conductor is hollow, with an inner radius R2 and outer radius R3.
- Both conductors carry equal currents I in opposite directions.
- Ampere's law states that the line integral of the magnetic field B around a closed loop is equal to μ0 times the current enclosed by that loop:
∮B⋅dl=μ0Ienc
- For a circular loop of radius r inside the inner conductor, the enclosed current Ienc can be calculated using the ratio of areas:
Ienc=I⋅AloopAtotal=I⋅πr2πR21=I⋅r2R21
- Applying Ampere's law:
B⋅2πr=μ0I⋅r2R21
- Solving for B:
B=μ0Ir2πR21
- This shows that B is directly proportional to r for r<R1.
- For a loop in the air gap between the inner and outer conductors, the enclosed current is just I (the current in the inner conductor):
B⋅2πr=μ0I
- Solving for B:
B=μ0I2πr
- This indicates that B is inversely proportional to r for R1<r<R2.
- For r>R3, the total current enclosed is zero because the currents in the inner and outer conductors cancel each other out:
B⋅2πr=0⟹B=0
- For r<R1: B increases linearly with r.
- For R1<r<R2: B decreases inversely with r.
- For r>R3: B=0.
The variation of the magnetic field with distance from the axis can be summarized as:
- Increases linearly for r<R1
- Decreases inversely for R1<r<R2
- Becomes zero for r>R3
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Sphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
View SolutionSphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
View SolutionIn a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
View SolutionThe figure shows a long straight current carrying conductor. Can you plot the variation of magnetic field on x-axis ?
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View SolutionConsider a co axial cable which consists of an inner wilre of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire caries a current I and outer shell carries an equal and opposite current. The magnetic field at a distance x from the axis where b<x<c is
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R.The distance r<R.The electric potential at the centre of the shell will be

View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View Solution
