Two infinitely long linear conductors are arranged perpendicular to each other and are in mutually perpendicular planes as shown in Fig. If I1=2A along the y-axis, I2=3A, along -ve z-axis and AP=AB=1cm, the value of magnetic field strength →B at P is

(3×10−5T)ˆj+(−4×10−5T)ˆk
(3×10−5T)ˆj+(4×10−5T)ˆk
(4×10−5T)ˆj+(−4×10−5T)ˆk
(−3×10−5T)ˆj+(4×10−5T)ˆk
The correct Answer is:B
(b) Magnetic field strength at P due to I1
→B1=μ0I2π(AP)ˆk=4π×10−7×22π×1×10−2ˆk=(4×10−5T)ˆk
Magnetic field strength at P due the I2
→B2=μ0I22π(BP)ˆj=4π×10−7×32π×2×10−2ˆj=(3×10−5T)ˆj
Hence, →B=(3×10−5T)ˆj+(4×10−5T)ˆk
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
A circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.

View SolutionTwo long mutually perpendicular conductors carrying currents I1 and I2 lie in one plane, Find the locus of points at which the magnetic induction is zero.
View SolutionA long straight wire carrying current i=10A lies along y-axis. Find the magnetic field at P(3cm, 2cm,4cm).

View SolutionThree infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.
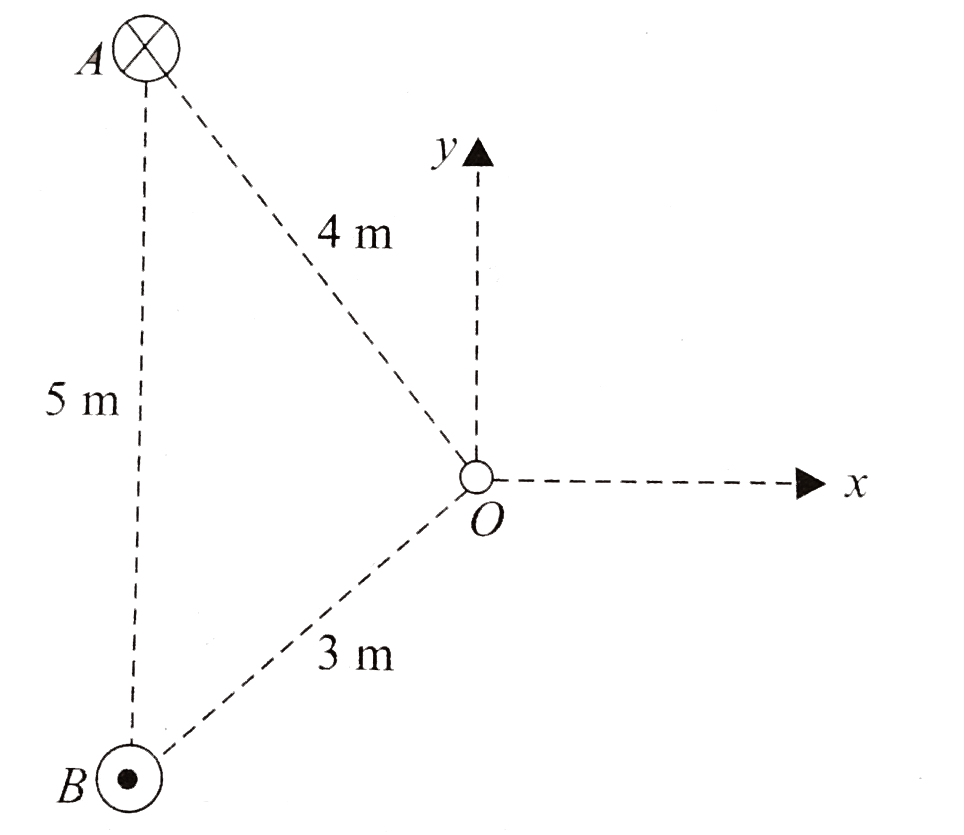
View SolutionTwo infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
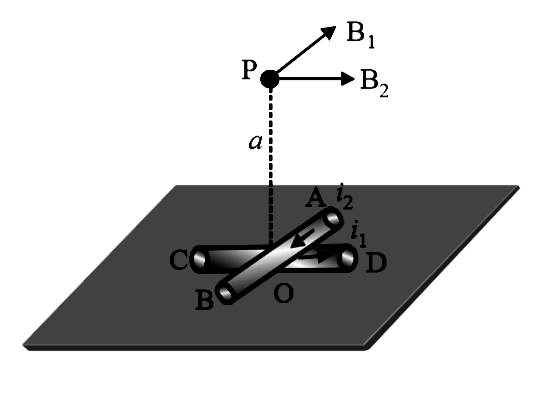
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is

View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
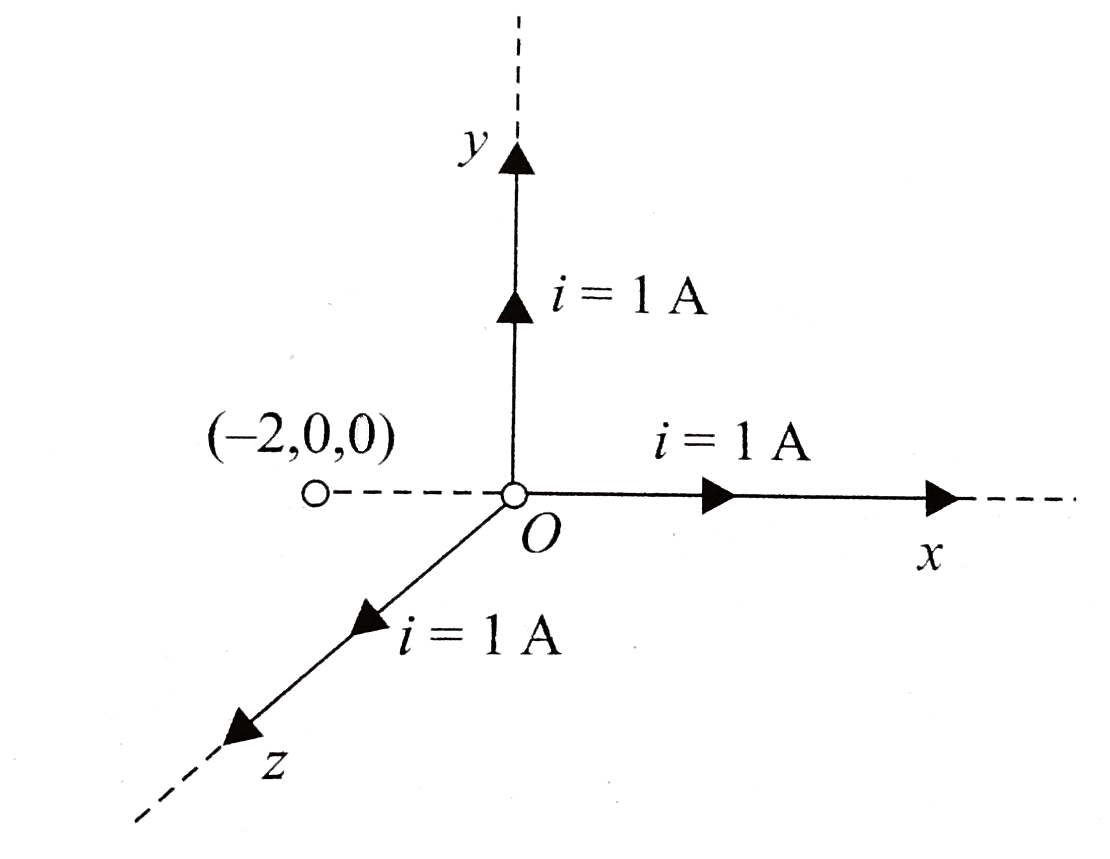
View SolutionLet →b=4ˆi+3ˆjand→c be two vectors perpendicular to each other in the xy-plane. Find all vetors in te same plane having projection 1 and 2 along →band→c respectively.
View Solution