Two protons move parallel to each other with an equal velocity v=300kms−1. Find the ratio of forces of magnetic and electric interaction of the protons.
The correct Answer is:1.00×10−6
To find the ratio of the forces of magnetic and electric interaction of two protons moving parallel to each other with a velocity v=300km/s, we can follow these steps:
Step 1: Identify the Electric Force
The electric force Fe between two protons can be calculated using Coulomb's law:
Fe=k⋅e2r2
where k=14πϵ0 is Coulomb's constant, e is the charge of a proton (e≈1.6×10−19C), and r is the distance between the two protons.
Step 2: Identify the Magnetic Force
The magnetic force Fm between two moving charges can be calculated using the formula:
Fm=μ04π⋅e2⋅v2r2
Here, μ0 is the permeability of free space.
Step 3: Calculate the Ratio of Forces
To find the ratio of the magnetic force to the electric force, we can express it as:
FmFe=μ04π⋅e2⋅v2r214πϵ0⋅e2r2
This simplifies to:
FmFe=μ0⋅v2ϵ0
Step 4: Use the Relationship Between μ0, ϵ0, and c
We know that:
μ0ϵ0=1c2
where c is the speed of light in vacuum (c≈3×108m/s). Therefore, we can rewrite the ratio as:
FmFe=v2c2
Step 5: Substitute the Values
Substituting v=300km/s=300×103m/s:
FmFe=(300×1033×108)2
Calculating this gives:
FmFe=(3003×105)2=(11000)2=1106
Conclusion
Thus, the ratio of the magnetic force to the electric force is:
FmFe=1:106
The electric force Fe between two protons can be calculated using Coulomb's law:
Fe=k⋅e2r2
where k=14πϵ0 is Coulomb's constant, e is the charge of a proton (e≈1.6×10−19C), and r is the distance between the two protons.
The magnetic force Fm between two moving charges can be calculated using the formula:
Fm=μ04π⋅e2⋅v2r2
Here, μ0 is the permeability of free space.
To find the ratio of the magnetic force to the electric force, we can express it as:
FmFe=μ04π⋅e2⋅v2r214πϵ0⋅e2r2
This simplifies to:
FmFe=μ0⋅v2ϵ0
We know that:
μ0ϵ0=1c2
where c is the speed of light in vacuum (c≈3×108m/s). Therefore, we can rewrite the ratio as:
FmFe=v2c2
Substituting v=300km/s=300×103m/s:
FmFe=(300×1033×108)2
Calculating this gives:
FmFe=(3003×105)2=(11000)2=1106
Thus, the ratio of the magnetic force to the electric force is:
FmFe=1:106
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (single Correct )
75 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Find the ratio of the electric and gravitational forces between two protons.
View SolutionTwo electrons move parallel to each other with equal speed 'V' the ratio of magnetic & electric force between them is
View SolutionIf two steams of proton move parallel to each other in the same direction, then they
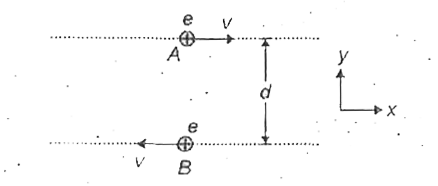
View SolutionTwo protons A and B move parallel to the x-axis is opposite directions with equal speed v. At the instant shown, the ratio of magnetic force and electric force acting on the proton A is (c=speed of light in vacuum)
View SolutionA proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionIf two protons are moving with speed v=4.5×105m/s parallel to each other then find the ratio of electrostatic and magnetic force between them : -
View SolutionA proton and an electron both moving with the same velocity v enter into a region of magnetic field directed perpendicular to the velocity of the particles. They will now move in cirular orbits such that
View SolutionA proton and a deuteron, each moving with velocity →v enter simultaneously in the region of magnetic field →B acting normal to the direction of velocity. Trace their trajectories establishing the relationship between the two.
View SolutionAn electron and a proton are moving on straight parallel paths with same velocity. They enter a semi infinite region of uniform magnetic field perpendicular to the velocity.
Which of the following statement(s) is /are true?
View SolutionAn electron and a proton are moving on straight parallel paths with same velocity. They enter a semi infinite region of uniform magnetic field perpendicular to the velocity.
Which of the following statement(s) is /are true?
View Solution
