In fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
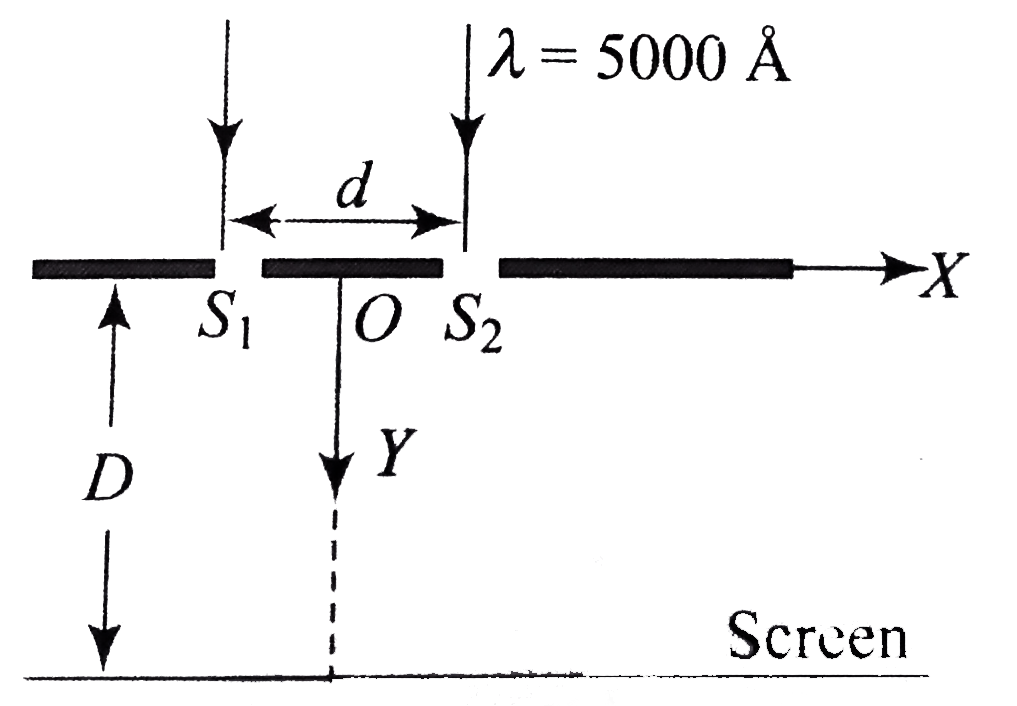
The velocity of central maxima at t=5s is
50ms−1 along Y-axis
50ms−1 along negative Y-axis
25ms−1 along Y-axis
3×108ms−1 along Y-axis
The correct Answer is:a
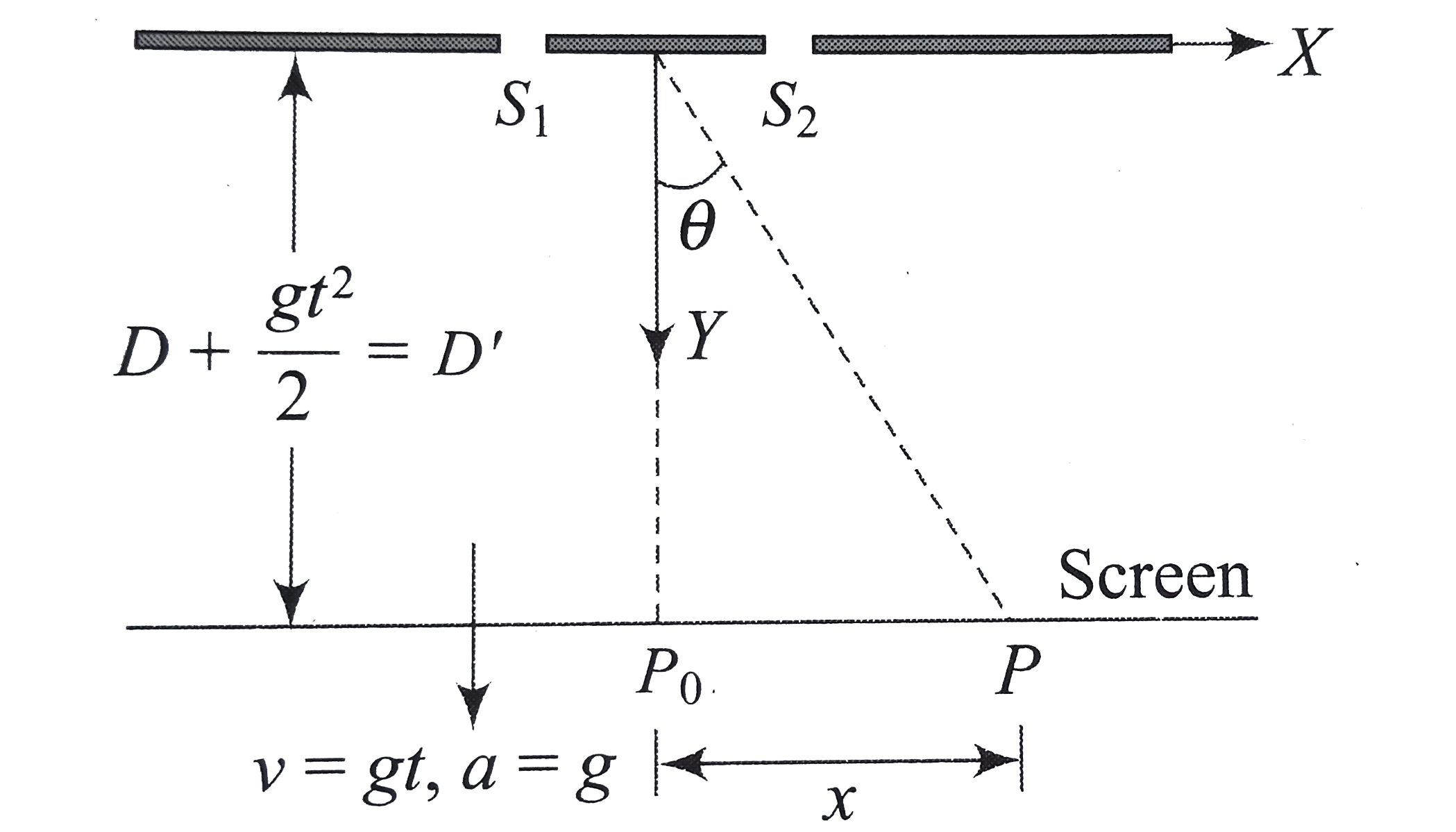
At any time t, the situation ia as shown in the figure below.
Central maxima is always lying on y-axis at P0. Its velocity at any time t is given by v p gt along positive Y-axis. So, required velocity is 50ms−1
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
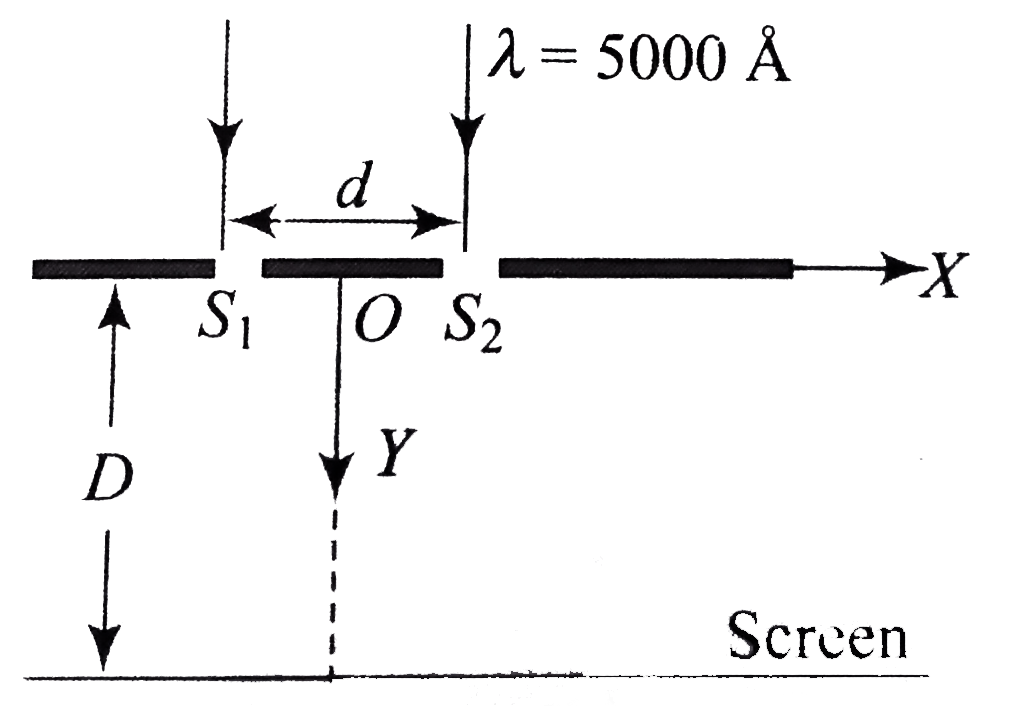
Velocity of 2nd maixma w.r.t central maxima at t=2s is
View SolutionIn fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
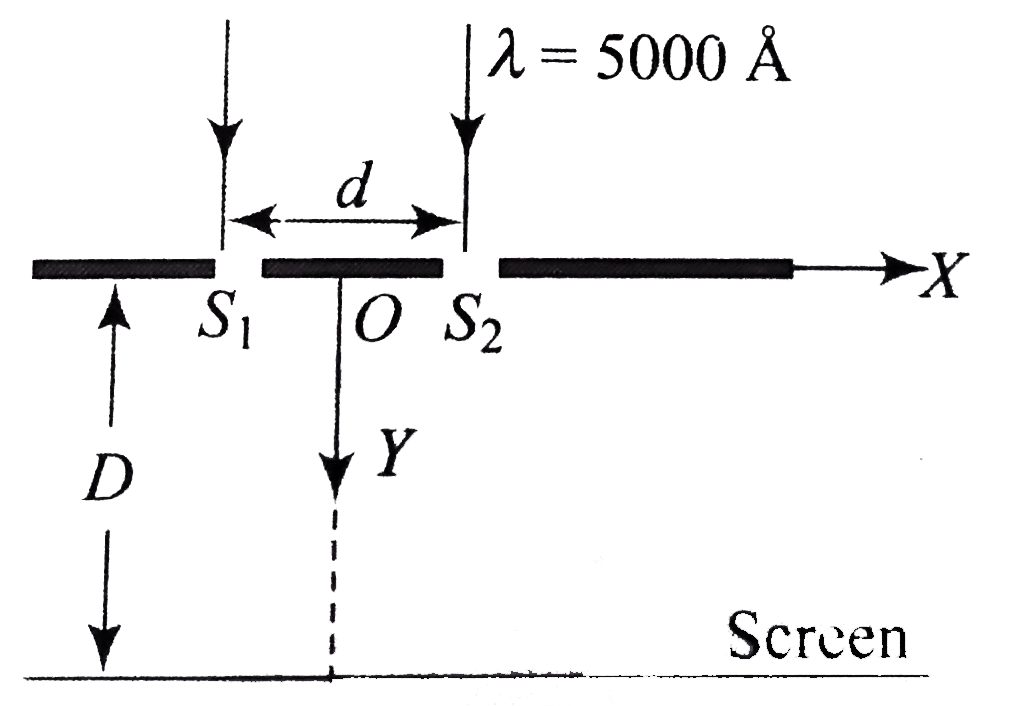
Acceleration of 3rd maxima w.r.t. 3rd maxiam on other side of central maxima at t=3 s is
View SolutionLight of wavelength 5000Å is incident over a slit of width 1μm. The angular width of central maxima will be
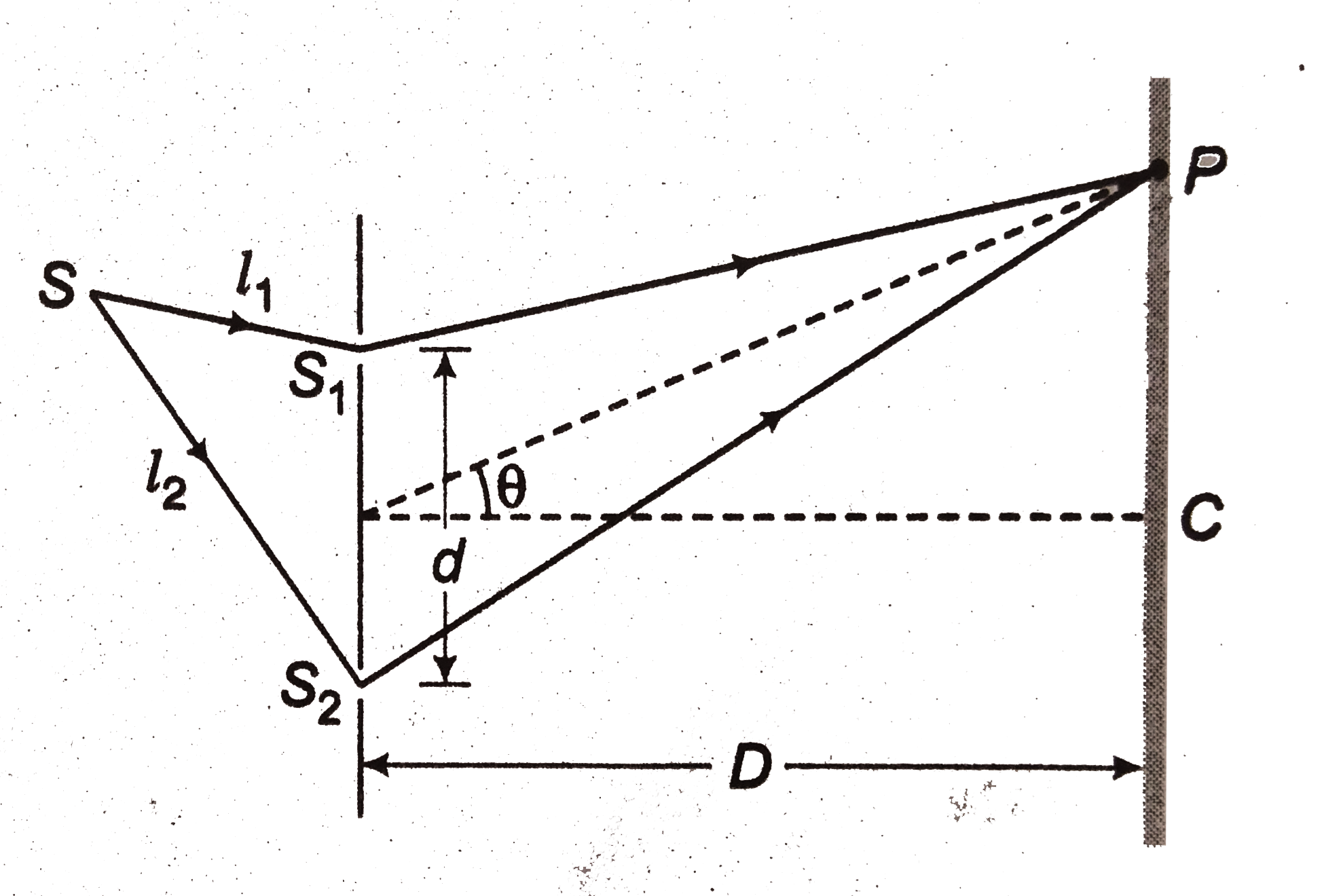
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .
.
View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View SolutionLight of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View SolutionLight of wavelength 5000A0 is incident on a slit. The first minimum of the diffraction pattern is observed to lie at a distance of 5 mm from the central maximum on a screen placed at a distance of 3 m from the slit. Then the width of the slit is
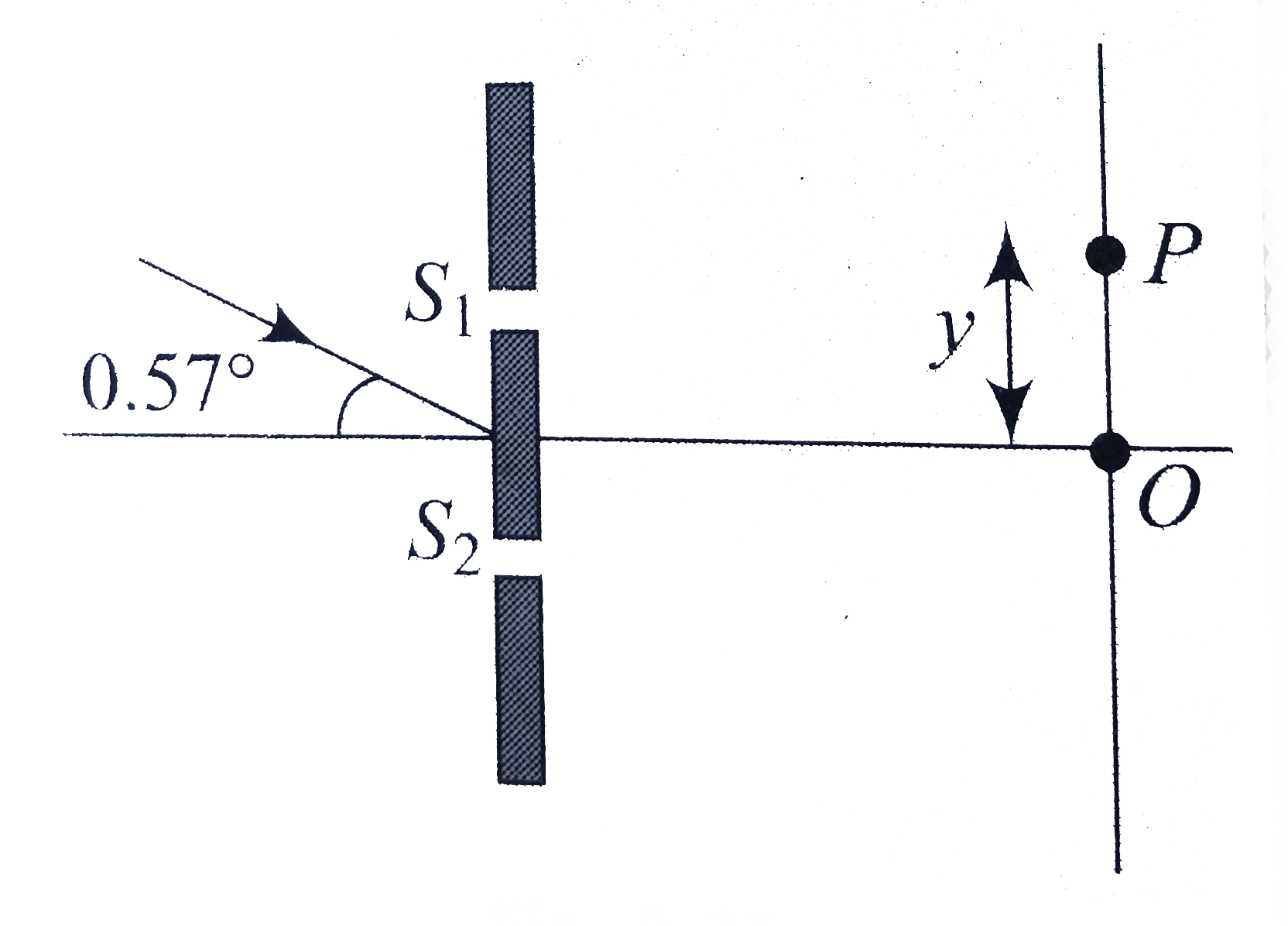
View SolutionIn YDSE with D=1m,d=1mm, light of wavelength 500nm is incident at an angle of 0.57∘ w.r.t. the axis of symmetry of the experimental set-up. If center of symmetry of screen is O as shown figure.
a. find the position of centrla maxima,
b. find intensity at point O in terms of intensity of central maxima I0, and
c. find number of maixma lying central maxima.
 .
.
View SolutionIn the arrangement shown in figure, light of wavelength 6000Å is incident on slits S1 and S2 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the closest position where intensity is same as that of the ligth used, below the central maximum Point O is equidistant from S1 and S2 and O' is equidistant from S3 and S4. Then intensity of inciden light is I0
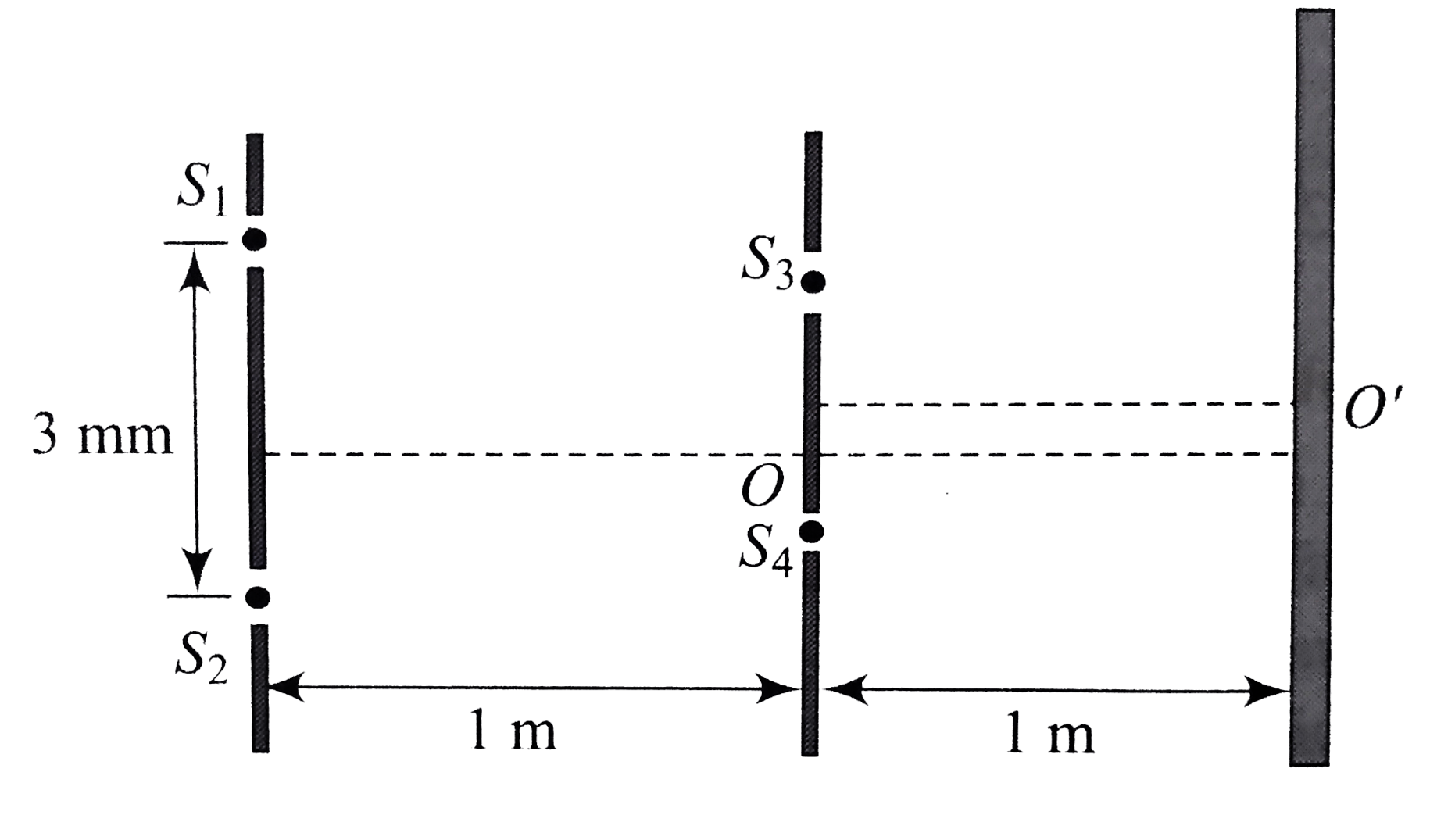
Find the intensity at O' (on the screen).
View Solution
