A conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?
(i) When S1 and S2 come in contact, there is transfer of charges till the potentials of the two spheres become equal. During first contact,
V1=V2(q1 charge shifts from S1 to S2)
⇒K(Q−q1)r=Kq1rR or q1=Q(RR+r)
During second contact, again
V1=V2
⇒K[Q−(q2−q1)]r=Kq2R
[(q2−q1)charge shifts fromS1toS2]
∴q2=Q[RR+r+(RR+r)2]
On third contact, again
V1=V2
⇒K[Q−(q3−q2)]r=Kq3R
[(q3−q2)charge shifts fromS1toS2]
∴q3=Q[RR+r+(RR+r)2+(RR+r)3]
On nth contact, by symmertry
V1=V2
⇒K[Q−(qn−qn−1)]r=KqnR
[(qn−qn−1charge shift fromS1toS2]
qn=Q[RR+r+(RR+r)2+...+(RR+r)n]
=QRr[1−(RR+r)n]
The eletrostatic energy of S2 after n contacts is
Un=12q2nC=12×14πε0R×{QRr[1−(RR+r)n]}2
(ii) The limiting value is
Ltn→∞Un=Ltn→∞[12×14πε0R{QRr[1−(RR+r)n]}2]
=Q2R2(4πε0)r2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.123videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.29videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
Match the refining methods (Column I) with (Column II).
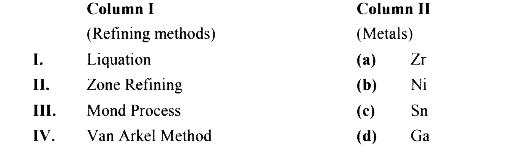 View Solution
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionSelf energy of conducting sphere of radius .r. carrying charge .Q. is ______
View SolutionA sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ratio of electric flux through S1andS2,
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

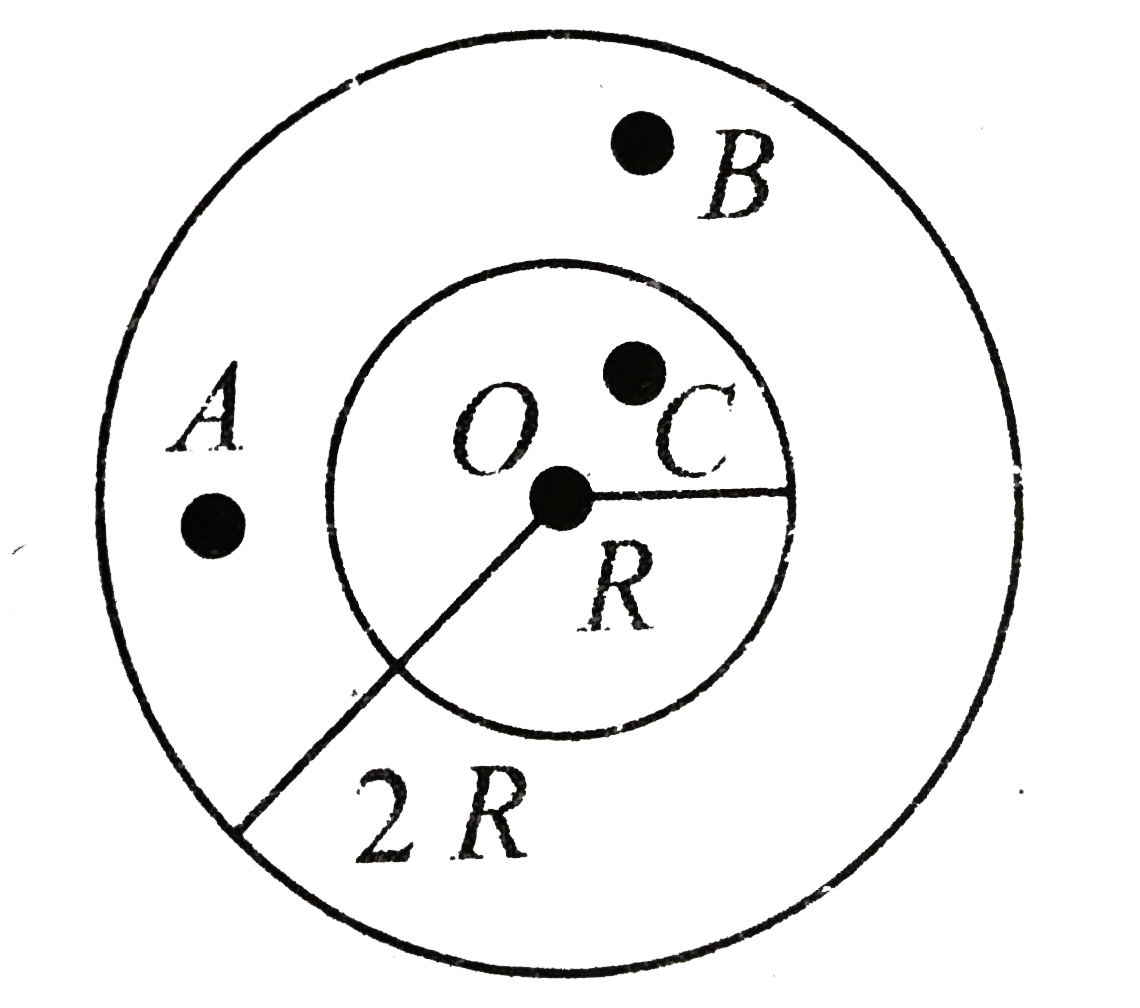
The final charge on initially neutral conducting sphere is :View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 View Solution
View SolutionA solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionTwo metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
View Solution
