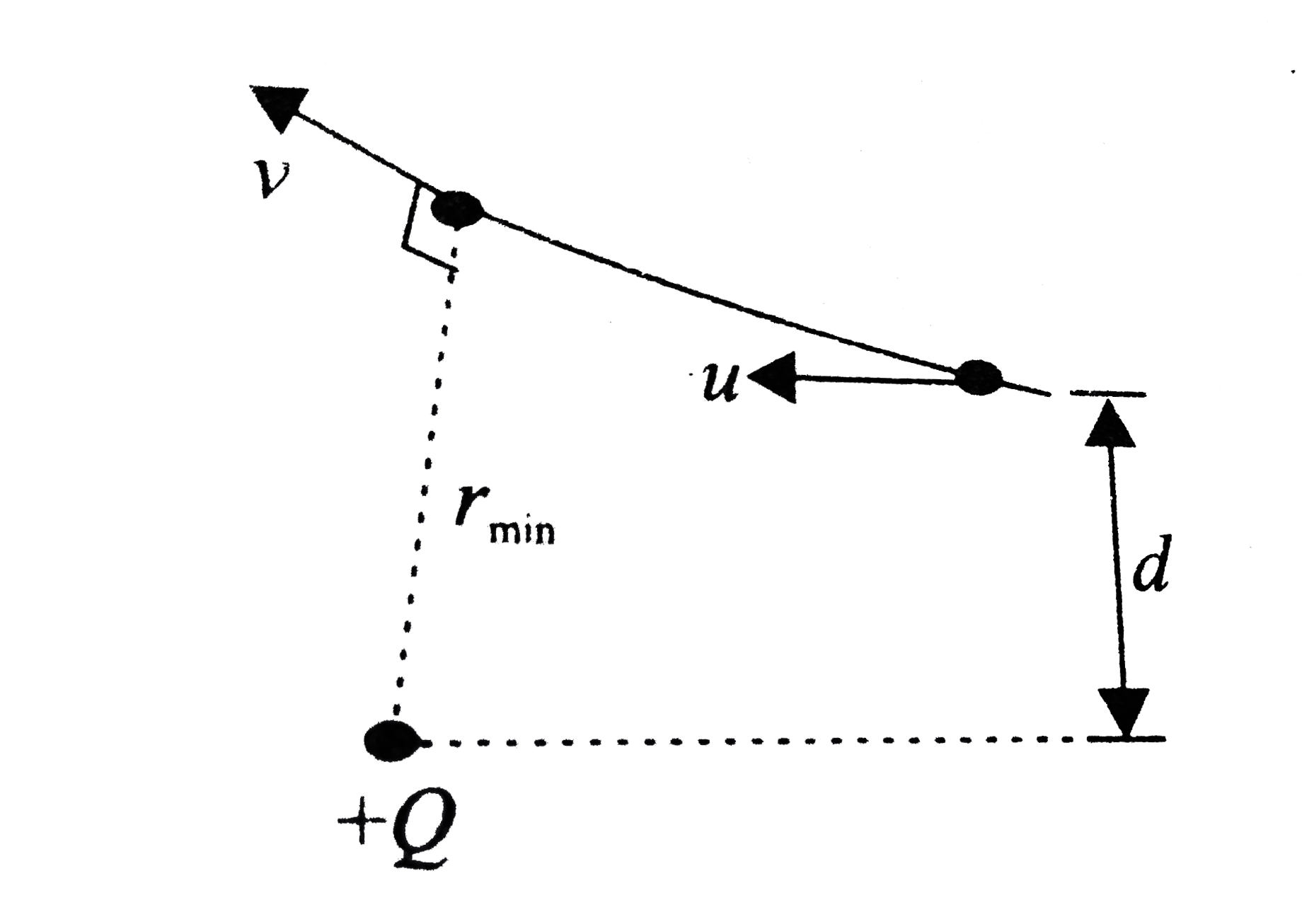
A positive charge +Q is fixed at a point A. Another positively charged particle of mass m and charge +q is projected from a point B with velocity u as shown in (Fig. 3.103). Point B is at a large distance from A and at distance d from the line A C. The initial velocity is parallel to the line A C. The point C is at a very large distance from A. Find the minimum distance (in meter) of +q from +Q during the motion. Take Qq=4πε0mu2d and d(√2−1)m.
 .
.
The path of the particle will be as shown in (fig. 3.104). At the point of minimum distance D, the velocity the particle will be ⊥ to its position vector with respect to +Q. Applying conservation of angular momentum, we get
 .
.
mud=mvrminorvrmin=ud
Now by conservation of energy
12mu2+0=12mv2+KQqrmin
or 12mu2(1−d2r2min=mu2drmin
[∵KQq=mu2d(given)]
or r2min−2rmind−d2=0
or rmin=2d±√4d2+4d22=d(1±√2)
Since distance cannot be negative
rmin=d(1+√2).
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.2
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

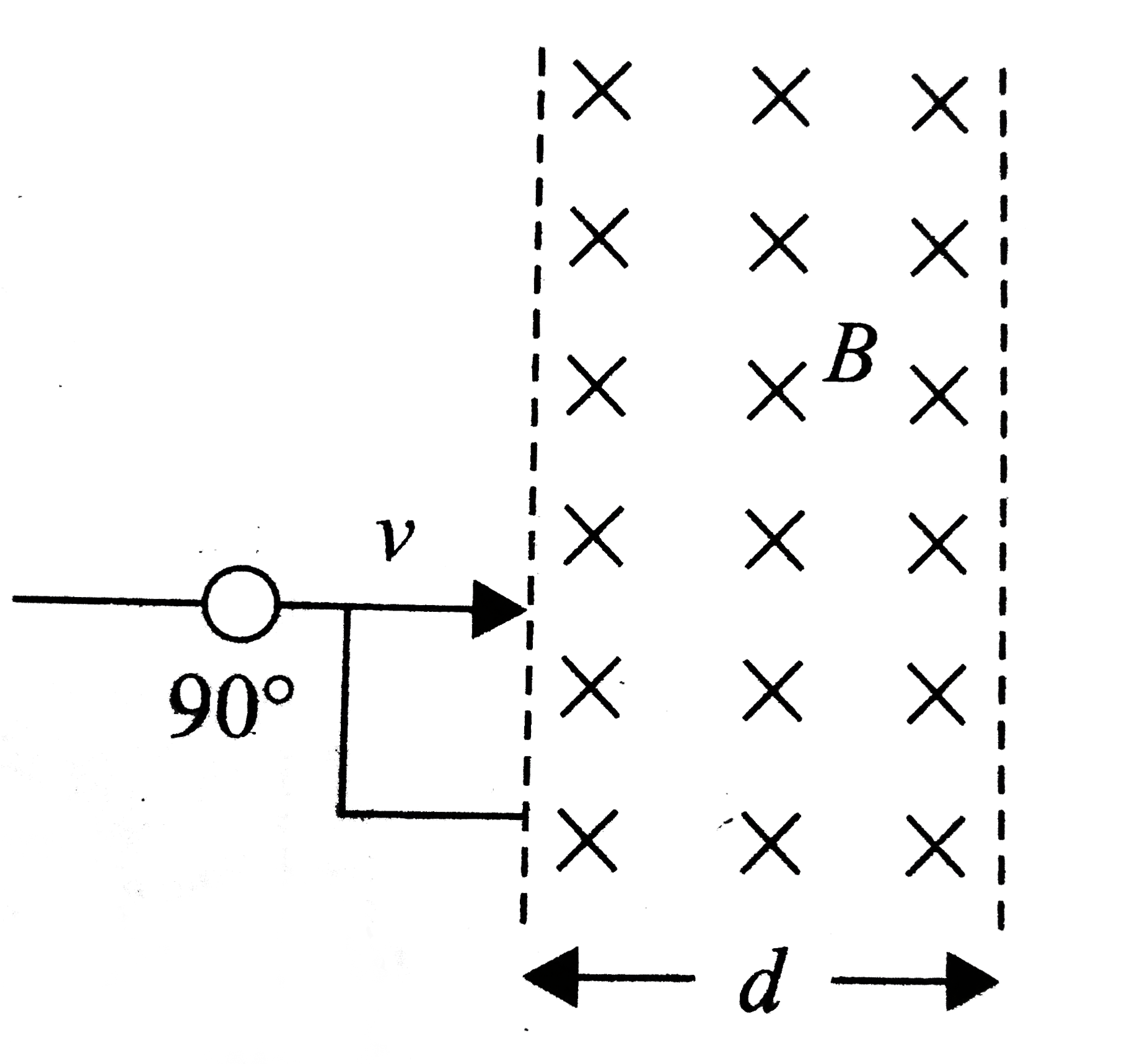
View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
View Solution
Knowledge Check
A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
Adirected perpendicular to the plane and away from the plane.Bdirected perpendicular to the plane but towards the plane.Cdirected radially away from the point charge.Ddirected radially towards the point charge.
A charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
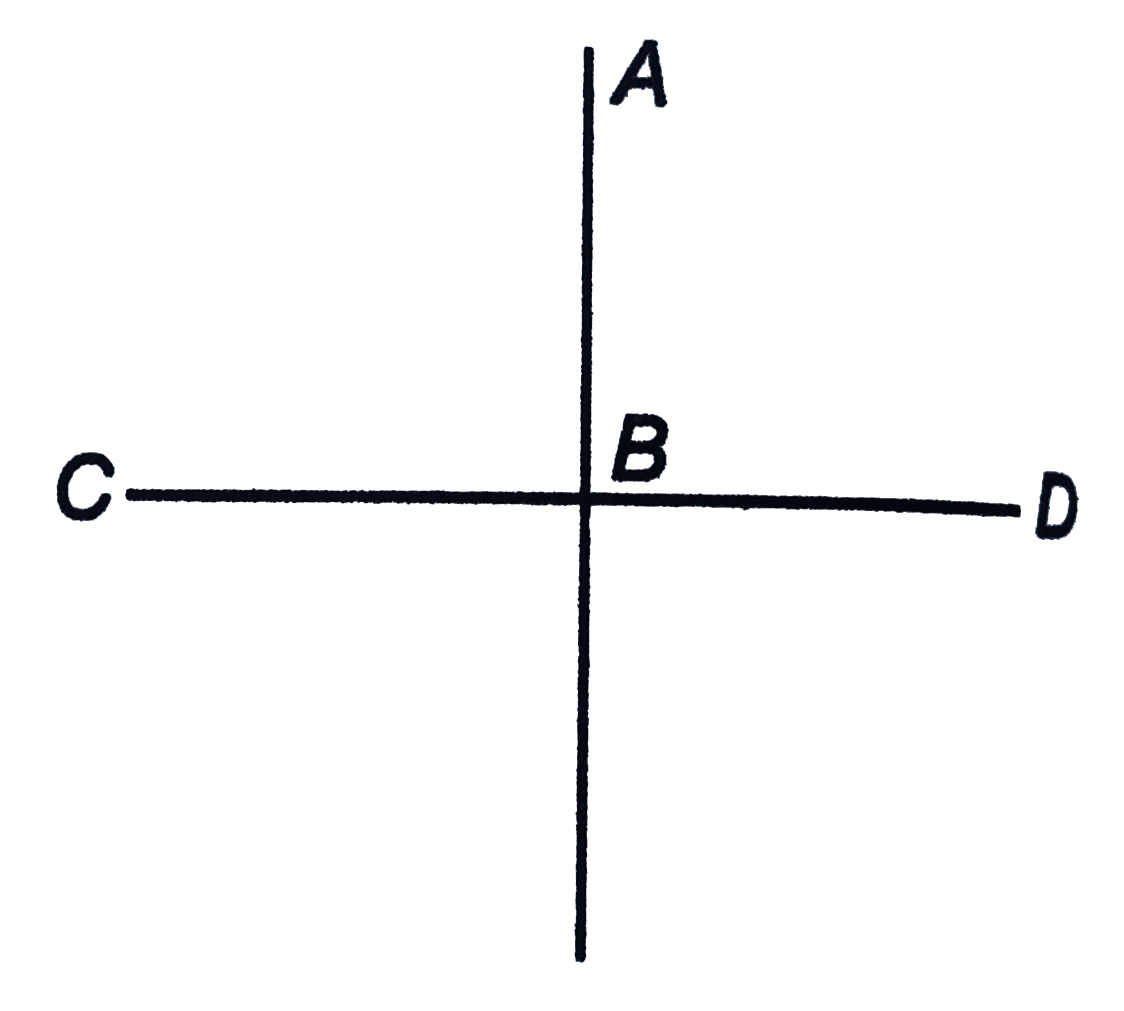
View SolutionTwo charges +Q each are fixed at points C and D. Line AB is the bisector line of CD. A third charge +q is moves from A to B, then from B to C
View SolutionA point charge +q is placed at origin O. The work done in taking another point charge -q from the point A to point B along the circular arc as shown in the figure is
_PHY_E05_122_Q01.png) .
.
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA non-relativistic charge q of mass m originates at a point A lying on x-axis and moves with velocity v at an angle to the x-axis. A screen is located at a distance l from A. Find the distance r from the x-axis to the point on the screen into which the charge strikes.

View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View Solution
