The potential in the electric field varies as V=−ax2+b with respect to x - coordinate, where a and b are constants. Find the charge density ρ(x) in a space.
The electric field E is present along x - axis because
∂V∂y=∂V∂z=0
Then, →E=−∂V∂xˆi=2axˆi …(i)
According to Gauss's law, the net flux of →E out of the cubical Gaussion surface is
E(x+dx)A−E(x)A=δqε0
or ∂E∂x.Aδx=δqε0
or ∂E∂x=1ε0(δqAδx)=ρ(x)ε0...(ii)
Using Eqs. (i) and (ii),
δδx(2ax)ˆi=ρ(x)ε0
or ρ(x)=2aε0.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Exercise 3.1
Explore 23 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Exercise 3.2
Explore 9 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
The electric potential in a region is given as V=−4ar2+3b, where r is distance from the origin, a and b are constants. If the volume charge density in the region is given by ρ=naε0, then what is the value of n?
View SolutionThe field potentail in a certain region of space depends only on the x coordinate as φ=−ax2+b, where a and b are constants. Find the distribution of the space charge ρ(x).
View SolutionFind the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
View SolutionThe potential energy of a particle varies with distance x from a fixed origin as V=A√XX+B where A and B are constants . The dimension of AB are
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionDetermine the electric field strength vector if the potential of this field depends on X, coordinates as V = 10 axy
View SolutionFind the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
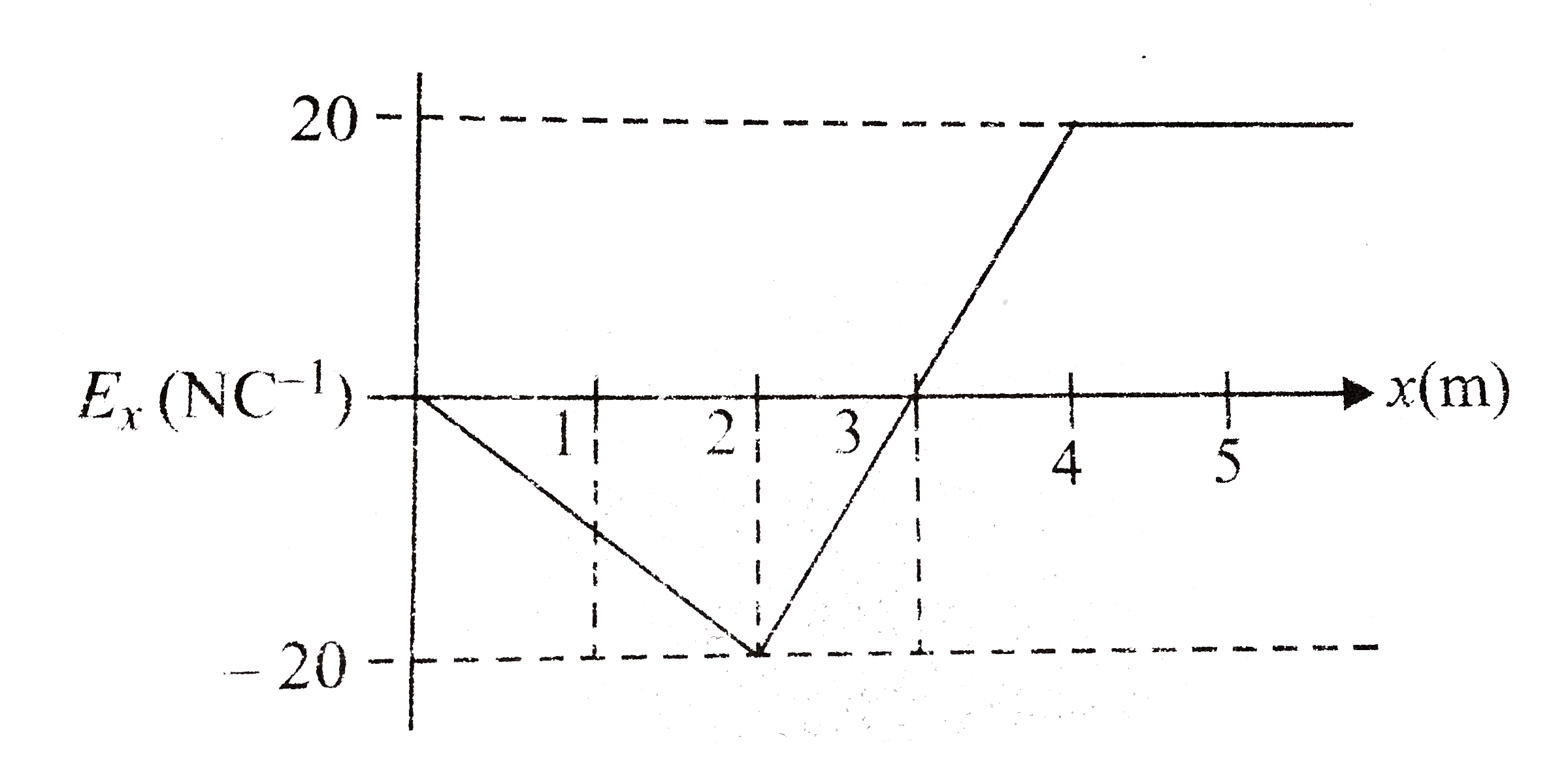
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
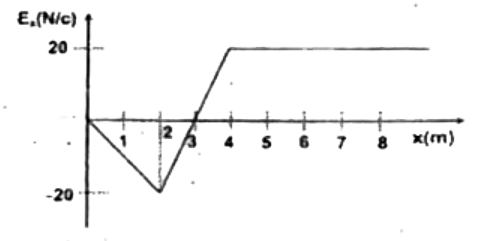
View SolutionA partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates xasU(x)=Ax2−Bx where A and B are positive constant.
Find the time period of small oscillation that the partical perform about equilibrium possition.
View Solution

