Two charge Q1=18μC and Q2=−2μC are separated by a distance R, and Q1 is on the left of Q2. The distance of the point where the net electric field is zero is
between Q1 and Q2
left of Q1atR/2
right of Q2 at R
right of Q2 at R/2
The correct Answer is:D
To find the point where the net electric field is zero due to two charges Q1=18μC and Q2=−2μC separated by a distance R, we can follow these steps:
Step 1: Understand the Configuration
- We have two charges, Q1 (positive) on the left and Q2 (negative) on the right.
- The distance between the charges is R.
Step 2: Identify Possible Locations for Zero Electric Field
- The electric field due to a positive charge points away from the charge, while the electric field due to a negative charge points towards the charge.
- The net electric field can potentially be zero either between the charges or outside the charges.
Step 3: Analyze the Region Between the Charges
- If we consider a point P between Q1 and Q2, the electric fields due to both charges will point in the same direction (away from Q1 and towards Q2), meaning they will add up and not cancel each other out. Therefore, the electric field cannot be zero between the charges.
Step 4: Analyze the Region Outside the Charges
- Consider a point P3 to the right of Q2. Here, the electric field due to Q1 will point to the left (away from Q1), and the electric field due to Q2 will also point to the left (towards Q2).
- Since Q1 is larger in magnitude than Q2, we can set up the equation for the electric fields.
Step 5: Set Up the Equation
- Let the distance from Q2 to point P3 be x. The distance from Q1 to point P3 will then be R+x.
- The electric field E1 due to Q1 at point P3 is given by:
E1=kQ1(R+x)2
- The electric field E2 due to Q2 at point P3 is given by:
E2=k|Q2|x2
Step 6: Set the Electric Fields Equal
- For the net electric field to be zero:
E1=E2
kQ1(R+x)2=k|Q2|x2
- Cancel k from both sides:
Q1(R+x)2=|Q2|x2
Step 7: Substitute the Values
- Substituting Q1=18×10−6C and |Q2|=2×10−6C:
18×10−6(R+x)2=2×10−6x2
- Cross-multiplying gives:
18x2=2(R+x)2
Step 8: Expand and Rearrange
- Expanding the right side:
18x2=2(R2+2Rx+x2)
18x2=2R2+4Rx+2x2
- Rearranging gives:
16x2−4Rx−2R2=0
Step 9: Solve the Quadratic Equation
- Using the quadratic formula x=−b±√b2−4ac2a:
- Here, a=16, b=−4R, and c=−2R2.
- Calculate the discriminant:
b2−4ac=(−4R)2−4⋅16⋅(−2R2)=16R2+128R2=144R2
- Thus:
x=4R±12R32
- This gives two solutions:
x=16R32=R2(valid solution)
x=−8R32(not valid)
Conclusion
- The point where the net electric field is zero is at a distance R2 from Q2 towards the right.
- We have two charges, Q1 (positive) on the left and Q2 (negative) on the right.
- The distance between the charges is R.
- The electric field due to a positive charge points away from the charge, while the electric field due to a negative charge points towards the charge.
- The net electric field can potentially be zero either between the charges or outside the charges.
- If we consider a point P between Q1 and Q2, the electric fields due to both charges will point in the same direction (away from Q1 and towards Q2), meaning they will add up and not cancel each other out. Therefore, the electric field cannot be zero between the charges.
- Consider a point P3 to the right of Q2. Here, the electric field due to Q1 will point to the left (away from Q1), and the electric field due to Q2 will also point to the left (towards Q2).
- Since Q1 is larger in magnitude than Q2, we can set up the equation for the electric fields.
- Let the distance from Q2 to point P3 be x. The distance from Q1 to point P3 will then be R+x.
- The electric field E1 due to Q1 at point P3 is given by:
E1=kQ1(R+x)2
- The electric field E2 due to Q2 at point P3 is given by:
E2=k|Q2|x2
- For the net electric field to be zero:
E1=E2
kQ1(R+x)2=k|Q2|x2
- Cancel k from both sides:
Q1(R+x)2=|Q2|x2
- Substituting Q1=18×10−6C and |Q2|=2×10−6C:
18×10−6(R+x)2=2×10−6x2
- Cross-multiplying gives:
18x2=2(R+x)2
- Expanding the right side:
18x2=2(R2+2Rx+x2)
18x2=2R2+4Rx+2x2
- Rearranging gives:
16x2−4Rx−2R2=0
- Using the quadratic formula x=−b±√b2−4ac2a:
- Here, a=16, b=−4R, and c=−2R2.
- Calculate the discriminant:
b2−4ac=(−4R)2−4⋅16⋅(−2R2)=16R2+128R2=144R2
- Thus:
x=4R±12R32
- This gives two solutions:
x=16R32=R2(valid solution)
x=−8R32(not valid)
- The point where the net electric field is zero is at a distance R2 from Q2 towards the right.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
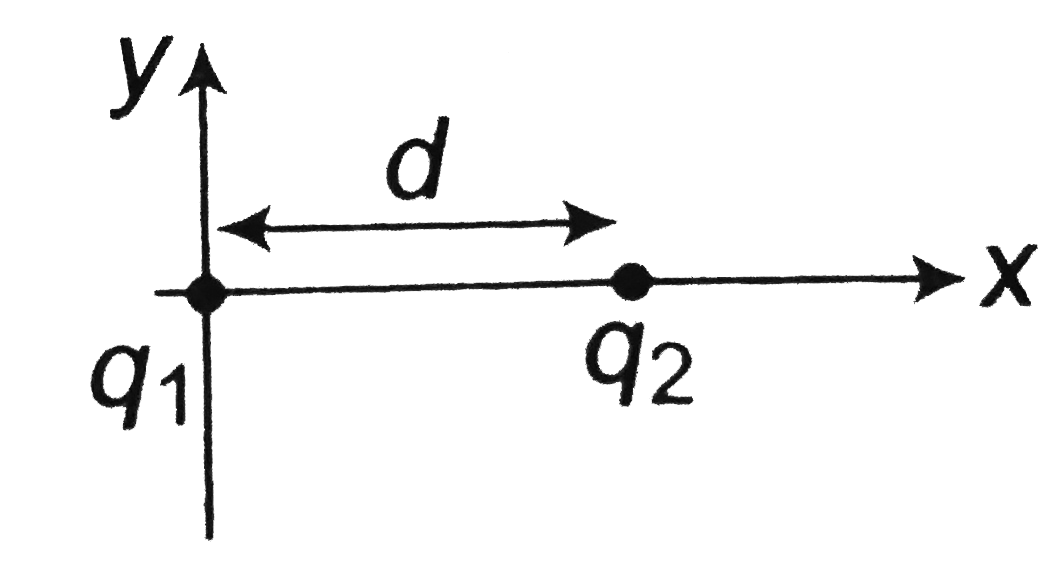
View SolutionTwo particles of charge q1 and q2 are separated by distance d as shown in figure. Chrage q1 is situarted at the origin. The net electirc field due to the particles is zero at x=d/4. With V=0 at infinity, the location of a point in terms of d on the x axis (other at infinfity) at which the elctrical potential due to the two particles is zero, is given by:
View SolutionTwo point charges, q1=10×10−8C and q2=−2×10−8C are separated by a distance of 60 cm in air.
(i) Find at what distance from the 1st charge, q1, would the electric potential be zero.
(ii) Also calculate the electrostatic potential energy of the system.
View SolutionTwo point charges q1=2×10−3C and q2=−3×10−6C are separated by a distance x=10 cm. Find the magnitude and nature of the force between the two charges.
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View SolutionTwo point charge q1=2μC and q2=1μC are placed at distance b=1 and a=2cm from the origin on the y and x axes as shown in figure .The electric field vector at point (a,b) will subtend on angle θ with the "x-axis" given by

View SolutionTwo point charge q1=2μC and q2=1μC are placed at distance b=1 and a=2cm from the origin on the y and x axes as shown in figure .The electric field vector at point (a),(b) will subtend on angle θ with the "x-axis" given by

View SolutionTwo point charges Q and -Q/4 are separated by a distance x.

View SolutionCharge 2qand−q are placed at (a,0)and(−a,0) as shown in the figure. The coordinates of the point at which electric field intensity is zero will be (x,0) where

View SolutionTwo charges q1=3.0μC and q2=−4.0μC initiallly are separated by a distance r0=2.0cm. An external agent moves the charges until they are rf=5.0cm apart. How much work is done by the electric field in moving the charges from r0 to rf ? Is the work positive or negative ?
View Solution
