An oil drop, carrying six electronic charges and having a mass of 1.6×10−12g, falls with some terminal velocity in a medium. What magnitude of vertical electric field is required to make the drop move upward with the same speed as it was formerly moving down ward with ? Ignore buoyancy.
105NC−1
104NC−1
3.3×104NC−1
3.3×105NC−1
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the oil drop and use the relevant equations.
Step 1: Understand the Forces Acting on the Oil Drop
When the oil drop is falling with terminal velocity, the forces acting on it are:
- The gravitational force (weight) acting downwards: Fg=mg
- The drag force acting upwards: Fd
At terminal velocity, these forces are equal:
Fd=mg
Step 2: Calculate the Weight of the Oil Drop
Given:
- Mass of the oil drop, m=1.6×10−12g=1.6×10−15kg (conversion from grams to kilograms)
- Acceleration due to gravity, g=9.8m/s2
The weight of the oil drop is:
Fg=mg=(1.6×10−15kg)(9.8m/s2)
Fg=1.568×10−14N
Step 3: Set Up the Equation for the Electric Field
When the electric field is applied to make the drop move upwards with the same speed, the forces acting on it are:
- The electric force acting upwards: Fe=Q⋅E
- The drag force acting downwards: Fd
- The weight acting downwards: Fg
The equation of motion can be written as:
Fe=Fd+Fg
Since the drop is moving upward with terminal velocity, we can express Fd as Fd=mg (because it balances the weight at terminal velocity):
Q⋅E=Fd+Fg
Q⋅E=mg+mg
Q⋅E=2mg
Step 4: Calculate the Charge on the Oil Drop
The oil drop carries 6 electronic charges. The charge of one electron is approximately e=1.6×10−19C.
Thus, the total charge Q is:
Q=6e=6×(1.6×10−19C)=9.6×10−19C
Step 5: Substitute Values into the Electric Field Equation
Now substituting Q into the equation:
E=2mgQ
Substituting the values:
E=2×(1.6×10−15kg)×(9.8m/s2)9.6×10−19C
Step 6: Calculate the Electric Field
Calculating the numerator:
2mg=2×1.6×10−15×9.8=3.136×10−14N
Now substituting this into the equation for E:
E=3.136×10−149.6×10−19
E≈3.27×104N/C
Step 7: Final Answer
Thus, the magnitude of the vertical electric field required to make the drop move upward with the same speed is approximately:
E≈3.27×104N/C
When the oil drop is falling with terminal velocity, the forces acting on it are:
- The gravitational force (weight) acting downwards: Fg=mg
- The drag force acting upwards: Fd
Fd=mg
Given:
- Mass of the oil drop, m=1.6×10−12g=1.6×10−15kg (conversion from grams to kilograms)
- Acceleration due to gravity, g=9.8m/s2
Fg=mg=(1.6×10−15kg)(9.8m/s2)
Fg=1.568×10−14N
When the electric field is applied to make the drop move upwards with the same speed, the forces acting on it are:
- The electric force acting upwards: Fe=Q⋅E
- The drag force acting downwards: Fd
- The weight acting downwards: Fg
Fe=Fd+Fg
Q⋅E=Fd+Fg
Q⋅E=mg+mg
Q⋅E=2mg
The oil drop carries 6 electronic charges. The charge of one electron is approximately e=1.6×10−19C.
Thus, the total charge Q is:
Q=6e=6×(1.6×10−19C)=9.6×10−19C
Now substituting Q into the equation:
E=2mgQ
E=2×(1.6×10−15kg)×(9.8m/s2)9.6×10−19C
Calculating the numerator:
2mg=2×1.6×10−15×9.8=3.136×10−14N
E=3.136×10−149.6×10−19
E≈3.27×104N/C
Thus, the magnitude of the vertical electric field required to make the drop move upward with the same speed is approximately:
E≈3.27×104N/C
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
An oil drop carrying a charge q has a mass m kg. it is falling freely in air with terminal speed v. the electric field required to make, the drop move upwards with the same speed is
View SolutionA water particle of mass 10.0 mg and having a charge of 1.50×10−6C stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View SolutionAn oil drop having a charge q and apparent weight W falls with a terminal speed v in absence of electric field . When electric field is switched on it starts moving up with terminal speed v. The strength of electric field is
View SolutionAn oil drop has a charge −9.6×10−19C and mass 1.6×10−15 gm. When allowed to fall, due to air resistance force it attains a constant velocity. Then if a uniform electric field is to be applied vertically to make the oil drop ascend up with the same constant speed, which of the following are correct. (g=10ms−2) (Assume that the magnitude of resistance force is same in both the cases)
View SolutionA charged oil drop falls with terminal velocity v0 in the absence of electric field. An electric field E keeps it stationary. The drop acquires charge 3q, it starts moving upwards with velocity v0. The initial charge on the drop is
View SolutionElectrons having a velocity →v of 2×106ms−1 pass undeviated through a uniform electric field →E of intensity 5×104Vm−1 and a uniform magnetic field →B.
(i) Find the magnitude of magnetic flux density B of the magnetic field.
(ii) What is the direction of →B, if →v is towards right and →E is vertically downwards in the plane of this paper ?
View SolutionIn Milikan's oil drop experiment, a charged drop falls with terminal velocity V. If an electric field E is applied in vertically upward direction then it starts moving in upward direction with terminal velocity 2V. If magnitude of electric field is decreased to E2, then terminal velocity will become
View SolutionIn 1909, Robert Millikan war the firest to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of opposite charged plates. The drops were pbserved with a magnitue eyepiece, and the electric field was adjusted so that upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of 1.6×10−19C− the charge of the electron. For this, he won the Nobel prize.
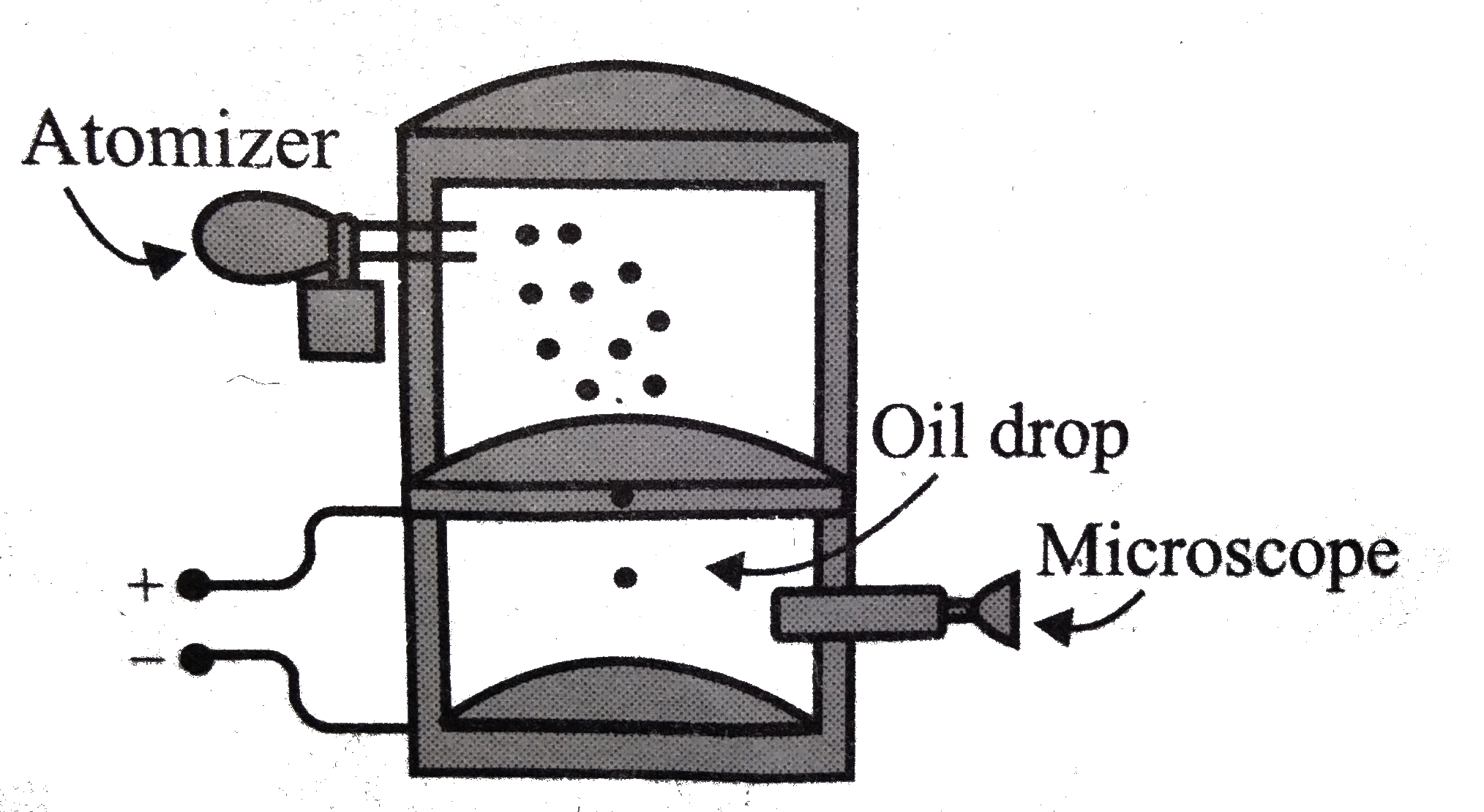
If a drop of mass 1.08×10−14kg remains stationary in an electric field of 1.68×105NC−1, then teh charge of this drop is
View SolutionCalculate the electric field strength required just to support a water drop of mass 10−7kg having a charge 1.6×10−19C
View SolutionCalculate the electric field strength which is required to just support a water drop of mass 10−3 kg and having a charge 1.6×10−19C.
View Solution
