A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
Mg
Mg−Vρg
Mg+πR2hρg
ρg(V+πR2h)
The correct Answer is:D
According to Archimedes' principle upthrust weight of the fluid displaced Fbottom−Ftop=Vρg
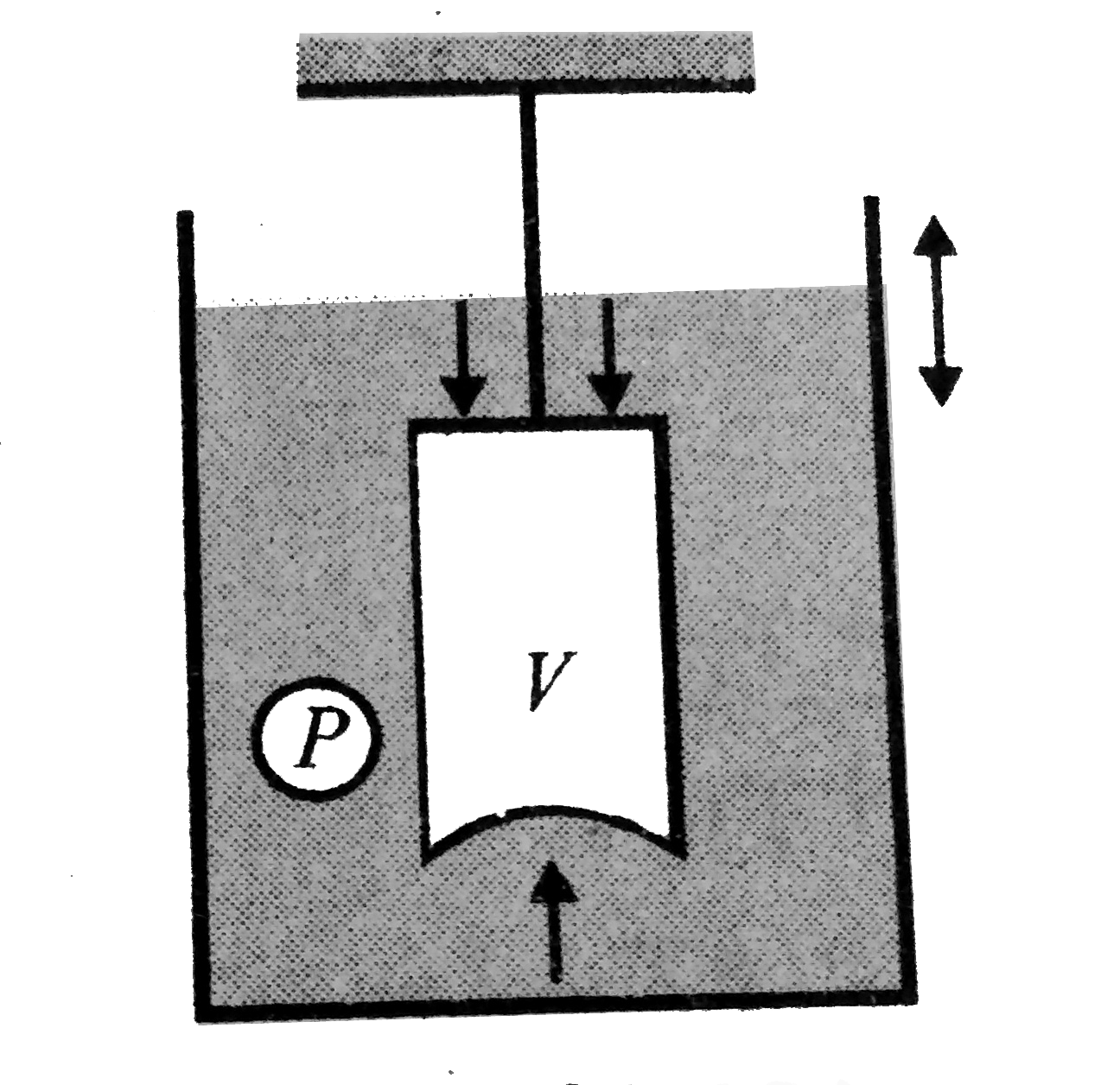
∴Fbottom=Ftop+Vρg
=P1×A+Vρg
=(hρg)×(πR2)+Vρg
=ρg[πR2h+V]
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:AR_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:MCQ_TYPE
Explore 3 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:True/False
Explore 1 Video
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
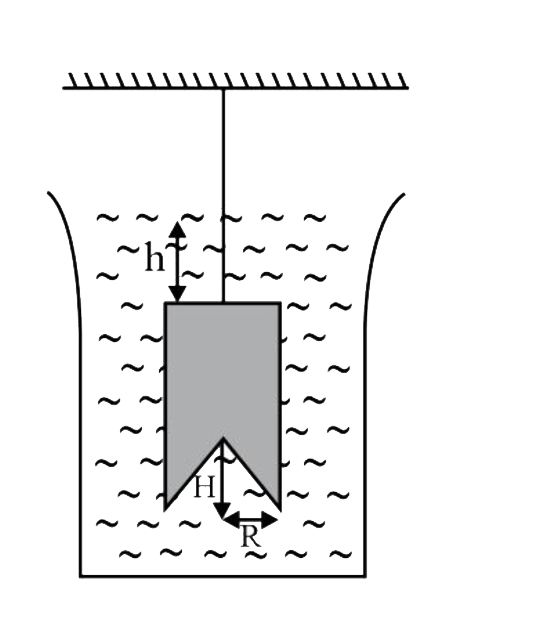
A conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
The radius of a cylinder is r and heigth is h. Find its volume.
View SolutionWrite the ratio of total surface area to the surface area of a cylinder of radius r and height h
View SolutionFrom a cylinder of radius R, a cyclinder of radius R/2 is removed, as shown . Current flowing in the remaning cylinder is l. magnetic field strength is :

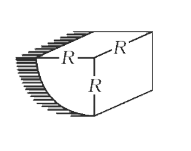
View SolutionA hollow cylinder of radius R and length R is cut into four equal parts from its axis. Each one is called quarter cylinder. If the quarter cylinder is just completely immersed in a liquid of density ρ, find the horizontal thrust acting on the curved surface of the cylinder.
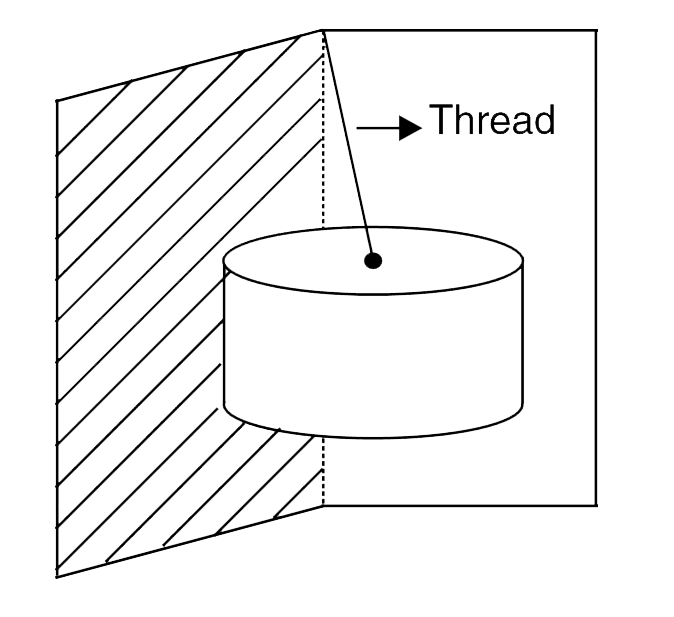
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
View SolutionThe ratio between the radius of the base and the height of a cylinder is 2:3., find the total surface area of the cylinder, it its volume is 1617 cm3.
View SolutionThe ratio between the radius of the base and the height of a cylinder is 2:3., find the total surface area of the cylinder, it its volume is 1617 cm3.
View Solution