A thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is
More than half-filled if , is less than
more than half-filled is more than ,
half filled if is more than
less than half-filled if is less than
The correct Answer is:D
To solve the problem of a thin uniform cylindrical shell that is partially filled with water and floating vertically in a half-submerged state, we will analyze the forces acting on the shell and the relationship between the densities involved.
1. Understanding the System:
- We have a cylindrical shell that is closed at both ends and is floating in water. It is partially filled with water and is in a vertical position, half-submerged.
- Let Vs be the volume of the shell, Vw the volume of water inside the shell, and Va the volume of air inside the shell.
2. Weight of the Shell:
- The weight of the shell can be expressed as:
Wshell=Vs⋅ρc⋅g
- Here, ρc is the density of the shell material, and g is the acceleration due to gravity.
3. Buoyant Force:
- The buoyant force acting on the shell is equal to the weight of the water displaced by the submerged part of the shell:
Fb=(Vw+Va)⋅ρw⋅g
- Here, ρw is the density of water.
4. Equilibrium Condition:
- For the shell to float in equilibrium, the weight of the shell must equal the buoyant force:
Wshell=Fb
- Substituting the expressions for weight and buoyant force, we have:
Vs⋅ρc⋅g=(Vw+Va)⋅ρw⋅g
5. Simplifying the Equation:
- Canceling g from both sides, we get:
Vs⋅ρc=(Vw+Va)⋅ρw
6. Volume Relationships:
- Since the shell is half-submerged, we can express the volumes as:
Vw+Va=Vs
- This implies that the total volume of the shell is equal to the sum of the volumes of water and air.
7. Analyzing Relative Density:
- The relative density ρc is defined as the ratio of the density of the shell material to the density of water:
ρc=Density of shellDensity of water
- If ρc<0.5, it indicates that the shell is less dense than half the density of water, meaning it is more buoyant and thus more than half-filled with water.
8. Conclusion:
- Therefore, if ρc<0.5, the shell is more than half-filled with water. If ρc>0.5, it would be less than half-filled.
- The correct statement is that the shell is more than half-filled if ρc<0.5.
Final Answer:
The shell is more than half-filled if ρc<0.5.
- We have a cylindrical shell that is closed at both ends and is floating in water. It is partially filled with water and is in a vertical position, half-submerged.
- Let Vs be the volume of the shell, Vw the volume of water inside the shell, and Va the volume of air inside the shell.
- The weight of the shell can be expressed as:
Wshell=Vs⋅ρc⋅g
- Here, ρc is the density of the shell material, and g is the acceleration due to gravity.
- The buoyant force acting on the shell is equal to the weight of the water displaced by the submerged part of the shell:
Fb=(Vw+Va)⋅ρw⋅g
- Here, ρw is the density of water.
- For the shell to float in equilibrium, the weight of the shell must equal the buoyant force:
Wshell=Fb
- Substituting the expressions for weight and buoyant force, we have:
Vs⋅ρc⋅g=(Vw+Va)⋅ρw⋅g
- Canceling g from both sides, we get:
Vs⋅ρc=(Vw+Va)⋅ρw
- Since the shell is half-submerged, we can express the volumes as:
Vw+Va=Vs
- This implies that the total volume of the shell is equal to the sum of the volumes of water and air.
- The relative density ρc is defined as the ratio of the density of the shell material to the density of water:
ρc=Density of shellDensity of water
- If ρc<0.5, it indicates that the shell is less dense than half the density of water, meaning it is more buoyant and thus more than half-filled with water.
- Therefore, if ρc<0.5, the shell is more than half-filled with water. If ρc>0.5, it would be less than half-filled.
- The correct statement is that the shell is more than half-filled if ρc<0.5.
The shell is more than half-filled if ρc<0.5.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - AR_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - MCQ_TYPE3videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
View SolutionA cylindrical tube, open at the both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of it is in water . The fundamental frequency of the air column is now-
View SolutionA shell of relative density 279 w.r.t water is just submerged in water. If its inner & outer radius is r and R then r/R is
View SolutionA shell of relative density 279 w.r.t water is just submerged in water. If its inner & outer radius is r and R then r is
View SolutionA cylindrical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now
View SolutionA cylindrical tube partially filled with water is in resonance with a tuning fork when height of air column is 0.1 m. When the level of water is lowered, the resonance is again observed at 0.35m. The end correction is –
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
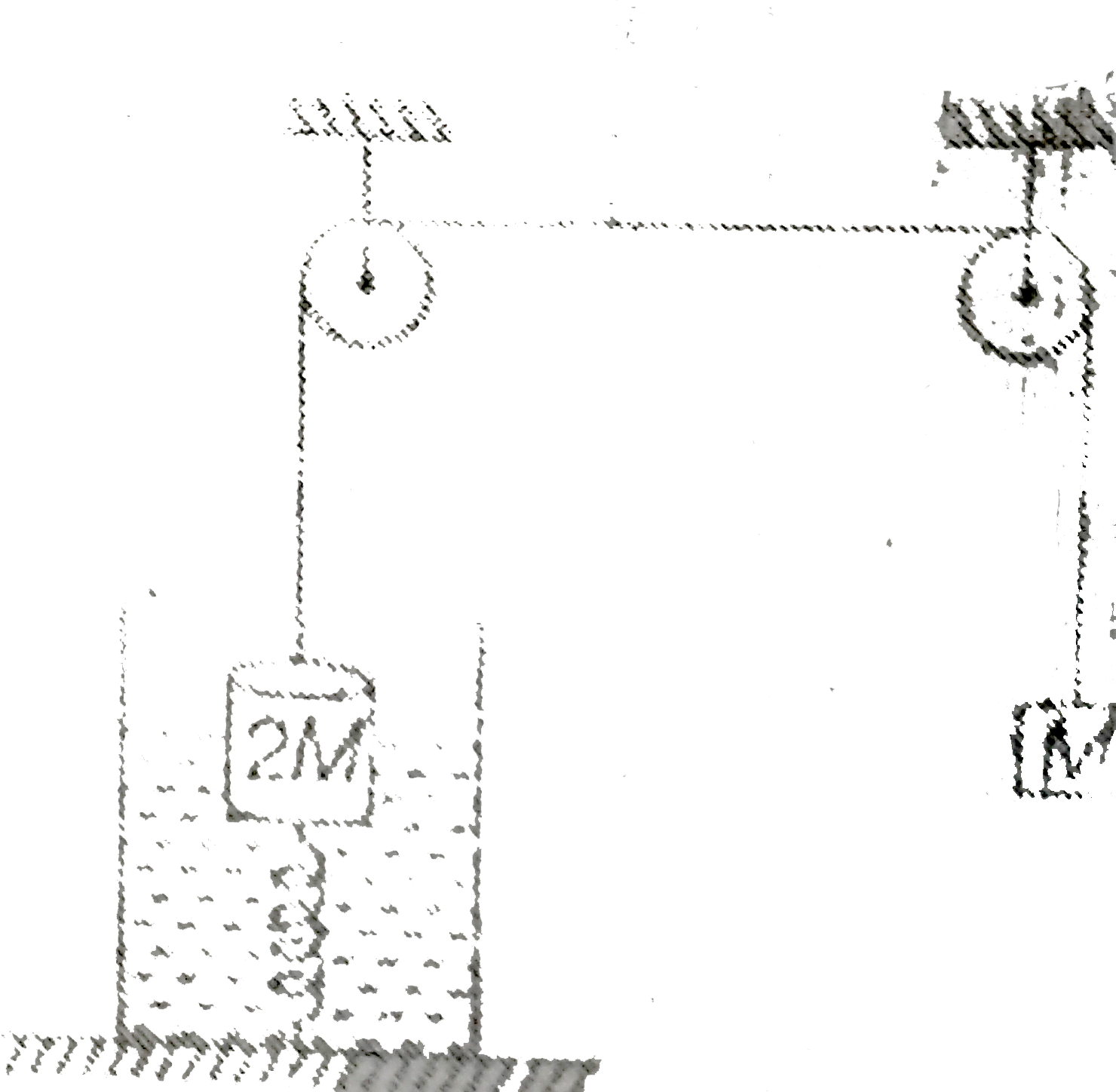 View Solution
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
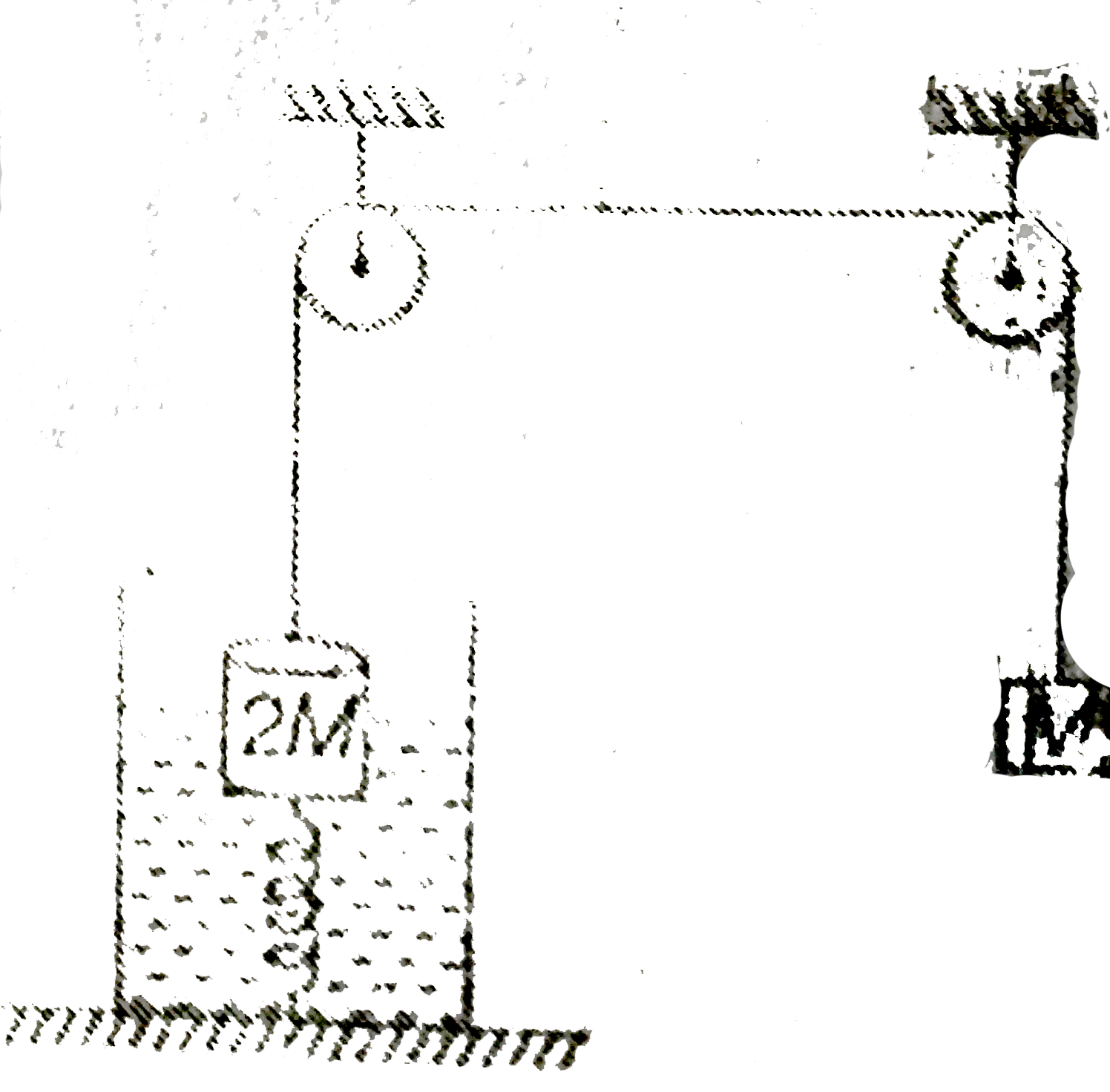
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]View Solution
