A large open tank has two holes in the wall. One is a square hole of side L at a depth h from the top and the other is a circular hole of radius R at a depth 4h from the top. When the tank is completely filled with water, quantities of water flowing out per second from both holes are the same. Then R is equal to
L/√2π
2πL
L
1/2π
The correct Answer is:A
Equating the rate of flow, we have
√(2gy)×L2=√(2g×4y)πR2
⇒L2=2πR2⇒R=L√(2π)
Flow =(area)×(velocity). Here Vel=√2gx
where x=ht from top
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - AR_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - MCQ_TYPE
3 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is circle of radius 'r'. The water flowing out per second from both the holes is same. Then 'L' is equal to
View Solution
Knowledge Check
A large open tank has two holes in the wall. One is square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth of 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then R is equal to
AL/√(2π)B2πLCLDL/2πA tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)
A vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is circle of radius 'r'. The water flowing out per second from both the holes is same. Then 'L' is equal to
View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View SolutionIn a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is

View SolutionThe bottom of a cylindrical vessel has a circlular hole of radius r and at depth h below the water] level. If the diameter of the vessel is D, the find then speed with which the water level in the] vessel drops.
View SolutionTwo holes 1 and 2 are made at depths h and 16h reapectively. Both the holes are circular but radius of hole-1 is two times.
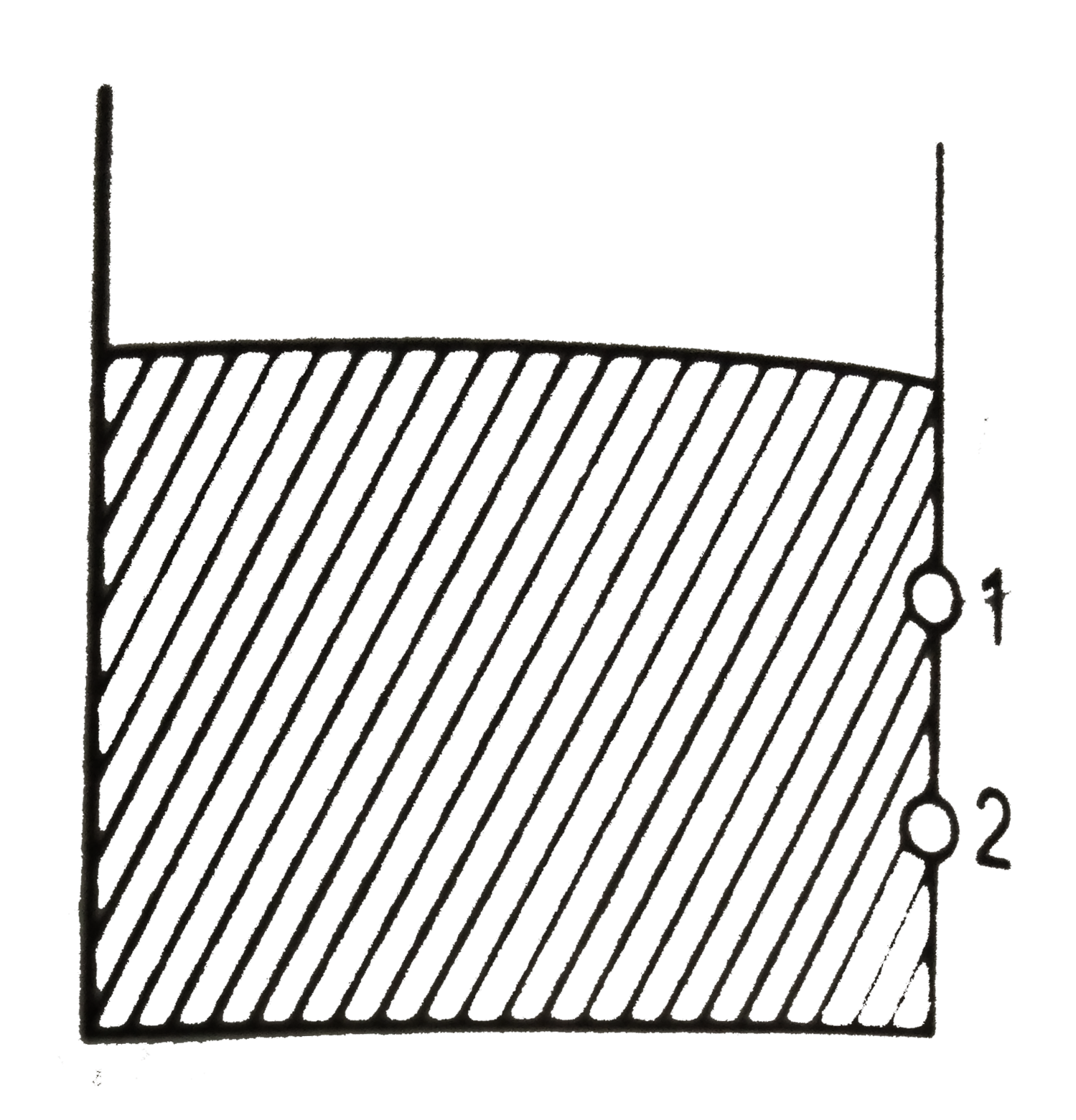
View SolutionA tank is filled with water and two holes A and B are made in it.- For getting same range, ratio of h' and h is
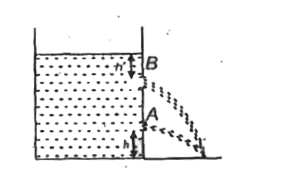
View Solution
